2002.11.29 — 2010.12.15
When a primitive is drawn grid cells are replaced with the primitive's colour or left unchanged. Its edges are jagged because of this all-or-nothing approach of filling in grid cells [7]. Aliasing is a term used to describe the jagged appearance. The application of methods to reduce aliasing is known as antialiasing.
Consider, for the moment, a three-dimensional scene where colour variations are complex and numerous. The projection of the objects onto the view plane yields a continuous signal whose value at each infinitesimal point represents the colour at that point. Sampling is the process of selecting a finite set of these values. Ideally, the sampling frequency must be more than twice the frequency of the signal to be sampled. This frequency is known as the Nyquist rate [11]. Supersampling and multisampling are popular sampling schemes to ensure we exceed the Nyquist rate. Details will be discussed shortly but, first, let's see how these samples are put to use.
By digitising the continuous signal into a finite set of samples there is a loss of information due to the nature of quantisation. Before we can assign intensities to each grid cell, we must reconstruct the original signal from the samples. If we do not attempt to recreate the signal and just display the samples as is, the result is very likely an image with a jagged appearance along the interface of any two regions. Filtering is the process by which we attempt to recreate the original signal from the sampled signal by taking the weighted average of the intensities [2]. Assuming the frequency of sampling exceeds the Nyquist rate, the original signal is almost reproduceable.
There are three filters commonly used in signal processing; two of which can be directly applied in computer graphics to reconstruct the original signal. The box filter (nearest neighbour) is the least ideal filter. It is often used, however, due to its simplicity.
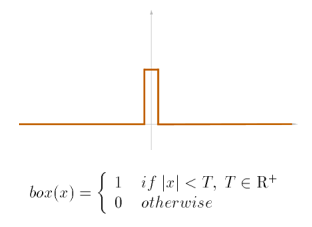
The area bounded by the x-axis and the function curve is known as thesupport of the filter. We scale the function so the support has an area of one. In other words, the weighted averaging of the sample(s) within the box filter produces a normalised intensity no greater than one. The box filter is placed over the sample(s) and scaled so the topmost point of the filter coincides with the sample. The reconstructed signal is the sum of these scaled and translated box filters [1]. You can improve the box filter's ability to recover the original signal by sampling at a much higher frequency than the Nyquist rate.
The tent filter (linear interpolation) does a better job at signal reconstruction. It is simple and easy to implement. The results are good in many situations but not perfect. The support of the filter is equal to one.
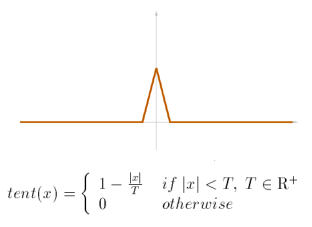
The filter is centered over the sample and scaled as needed. The reconstructed signal is the sum of the scaled and translated tent filters [1].
The most ideal filter, in theory, is the sinc filter. The original signal can be perfectly recreated from the samples when a sinc filter is applied. Because the filter has infinite spatial extent, it's impractical. One solution is to convolve the filter with, say, a box filter to remove the ripples.
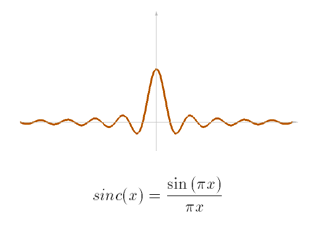
What we get is a windowed sinc filter, something we can now use. We can improve the quality of the windowed sinc filter by widening its extent at the cost of more arithmetic. As such, it's often sufficient just to use the box filter or tent filter.
Sampling an image more than once per grid cell is known as supersampling antialiasing (SSAA). Although several antialiasing methods exhibit some form of supersampling, there are important differences make some methods better than others. A particular supersampling technique makes four copies of the original image and stores these copies into separate image buffers. Each copy is offset in both the x- and y- directions. What you have is essentially four samples per cell, with one sample for each of the four quadrants. These samples are not necessarily centered in their respective regions, however. A common configuaration of four off-center samples is formally known as Rotated Grid Super Sampling (RGSS). NVIDIA Corporation implements transparency adaptive RGSS via Intellisample™ 4.0. This technology is available in their GeForce 7 series of graphical processing units (GPUs).
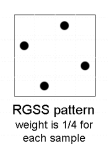
The contribution of each sample is one-quarter of its intensity. The cost of this scheme is threefold. First, the display hardware must have several buffers to store the jittered versions of the original contents of the framebuffer. Second, antialiasing is performed on the entire image regardless of where the aliasing actually exists. And, lastly, the contents of the auxiliary buffers must be combined to yield to final image. An issue with most supersampling methods is that they use a box filter having a support no greater than the width of one grid cell. The samples, as a result, can only affect one grid cell thereby capping their ability to provide high-quality signal reconstruction. Although supersampling yields good results, the method is very computationally demanding.
A supersampling scheme where the samples are distributed in a quasi-random manner is known as stochastic sampling. This unintuitive scheme can actually yield impressive results because it exploits our inability to readily distinguish random patterns against a backdrop of varying signals. We commonly refer to and dismiss these seemingly random patterns as signal noise. Implementations of stochastic sampling apply a different sampling template to each grid cell.
This method applies the same arrangement of samples for each gird cell. If a grid cell is partitioned into n regions of equal area we have an n x n array of subcells. The samples are placed so that each of these subcells has exactly one sample.
An antialiasing method is said to use interleaved sampling if the sampling pattern is the same for only a small set of contiguous grid cells. Implementations of interleaved sampling define up to 16 unique sampling templates. Each template consists of up 16 samples that are distributed in a non-grid fashion.
Another ingenious method that ensures sampling above the Nyquist rate is called multisampling antialiasing (MSAA). Only partially covered grid cells are sampled more than once and filtered accordingly. The use of coverage information is derived from Carpenter's A-buffer algorithm [6]. An early antialiasing method that uses multisampling is known as Accuview™. The sampling pattern is a Quincunx: four samples to denote the corners of a square and one sample in the center [9].
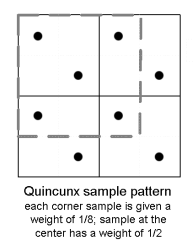
The weight given to each corner sample is 1/8. The center sample is given a weight of 1/2. This distribution of weights forms a tent filter. The support of the filter is 1.5 times the width of a grid cell. Each grid cell only has two samples; one in the north-west quadrant and the other in the south-east quadrant. The remaining three samples to form the Quincunx sample pattern are taken from the neighbouring grid cells to the east, south-east and south.
There are two sampling methods that blends the best features of supersampling (regular sampling pattern and box filter usage) and multisampling (only those grid cells that are partially covered by fragments are considered).
The samples in 4XS are arranged in a 2 x 2 array: four samples located in each of the four quadrants of a subdivided grid cell. For each sample we store the colour and depth information in buffers. The depth values are used to compute the weighted average of the top row of samples. A greater weight is assigned to samples that are closer to the camera. The next step involves calculating the weighted average of the bottom row of samples. And, lastly, we take the average of these two weighted averages. The result is the colour for that particular grid cell. Alternatively, we can compute the weighted average of both columns of samples and average the results.
The samples in 6XS are arranged in a 2 x 3 array: three rows of two samples. The grid cell is subdivided accordingly to yield six subcells of equal area. For each sample we store the colour and depth information in a buffer. During the filtering process the weighted average of each row of samples is computed. With these three weight averages, the last step takes the average of these three values to yield the final colour of the grid cell. If we alternate between 2 x 3 and 3 x 2 sampling configurations, what we get is quasi-interleaved multisampling.
In both the 4XS and 6XS schemes, the resultant intensities are stored as 128-bit quantities, 32 bits for each channel. Before sending these intensities to the display device, the antialiasing method applies gamma correction to these values. Section 1.2 Gamma Correction provides some details.
MSAA stores the colour, depth (from the camera) and coverage information of each sample in buffers. These values are used to compute the final colour of a grid cell. NVIDIA Corporation created a method called coverage sampling antialiasing (CSAA) that decouples the colour and depth values from the positions of each sample point. Under NVIDIA's 16x CSAA only four colour values are stored but fragment coverage information of 16 sample points is retained. The effect is we achieve accurate coverage information for a grid cell without the storage requirements of 16x MSAA. The image quality achieved with CSAA is better than MSAA for the same number colour samples stored in the frame buffer.
In late 2010, AMD introduced a new antialiasing mode that's equivalent to CSAA. Known as enhanced quality antialiasing (EQAA), the method takes a number of coverage samples independent of the colour and depth samples. The sample pattern used by EQAA can be customised at the application level.
Beginning with version 10.1, the DirectX API allows the application developer to implement custom antialiasing filters with pixel shaders. These custom filters can offer improved quality in certain cases where standard multisampling filters can have issues, such as with high-dynamic range rendering and deferred shading techniques. Consumer level graphics cards that support custom filters include the AMD Radeon HD 5000 and 6000 series and the NVIDIA GeForce GTX 400 and 500 series.
As paraphrased from the GNU General Public License "the following instances of program code are distributed in the hope that it will be useful, but without any warranty; without even the implied warranty of merchantability or fitness for a particular purpose." Please do not hesitate to notify me of any errors in logic and/or semantics.
Line segments are generated by some variant of the digital line drawing algorithm developed by J.E. Bresenham [4, 5]. The drawLine routine detailed herein assigns a colour to one grid cell per loop iteration. There have been many optimisations to the classic method, one of which is based on the observation that some sequences occur more often than others [8]. At least two methods exploit the parallelism in some computer architectures. The double-step algorithm and the symmetric double-step algorithm, in particular, yield a fourfold increase in runtime performance [10, 12, 13].
The coordinates of a line segment are floating-point values. The endpoints must be quantised to the appropriate integer value before the call to drawLine. The integer portion of a floating-point value can be retrieved using the formula i = int(f + 0.5). Adding 0.5 rounds the number to the nearest integer.
// -----------------------------------------------------
// Line.h
// -----------------------------------------------------
#ifndef __LINE_H__
#define __LINE_H__
#include <iostream>
#include <vector>
using namespace std;
typedef struct {
double r, g, b, a;
} Colour;
typedef struct {
int x, y;
Colour c;
} GridCell;
class Line
{
public:
Line();
~Line();
void draw(int, int, int, int, Colour);
vector<GridCell> getGridCells(void);
private:
int abs(int);
int sgn(int);
void plot(int, int, Colour);
vector<GridCell> gridCell;
};
inline int Line::abs(int a)
{
return (((a) < 0) ? -(a) : a);
}
inline int Line::sgn(int a)
{
return (((a) < 0) ? -1 : 1);
}
inline vector<GridCell> Line::getGridCells()
{
return gridCell;
}
#endif // __LINE_H__
// -----------------------------------------------------
// Line.cpp
// -----------------------------------------------------
#include "line.h"
Line::Line()
{
gridCell.clear();
}
Line::~Line() { }
void Line::draw(int x0, int y0, int x1, int y1,
Colour c)
{
int d, x, y, ax, ay, sx, sy, dx, dy;
dx = x1 - x0;
ax = abs(dx) << 1;
sx = sgn(dx);
dy = y1 - y0;
ay = abs(dy) << 1;
sy = sgn(dy);
x = x0;
y = y0;
if (ax > ay) {
d = ay - (ax >> 1);
while (x != x1) {
plot(x, y, c);
if (d >= 0) {
y += sy;
d -= ax;
}
x += sx;
d += ay;
}
} else {
d = ax - (ay >> 1);
while (y != y1) {
plot(x, y, c);
if (d >= 0) {
x += sx;
d -= ay;
}
y += sy;
d += ax;
}
}
plot(x1, y1, c);
}
void Line::plot(int x, int y, Colour c)
{
GridCell gc;
gc.x = x;
gc.y = y;
gc.c = c;
gridCell.push_back(gc);
}
Antialiasing yields intermediate colours alongside the interface of two regions. These calculated intensities are highly precise, often stored as 32-bit quantities for each of the red, green, blue and alpha channels. A problem arises if the display hardware is limited to 32-bits, total, where only eight bits are alotted per channel. A typical CRT, LCD or OLED device receives a particular voltage V for each of level of intensity. For some 8-bit intensity I, the display hardware sends
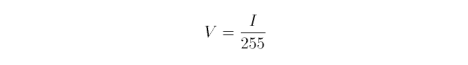
Although the voltage is a linear function of intensity, the actual display intensity, B, is dependent on two floating-point variables.
![]()
Brightness controls the gamma term, and contrast controls alpha (α). The gamma term varies between different display devices. As such, the digital artist has no way of ensuring the colours she chose is reproduced across all devices. Gamma correction is the process by which the intensities are adjusted to compensate for the mangling that occurs before grid cell illumination [3]. One solution is to modify our calculated intensity D to yield a gamma corrected intensity.
![]()
The adjustment provides more comfort to the artist, but more precise control is still needed to achieve absolute perfect colour reproduction. Intellisample™ from NVIDIA Corporation provides gamma-adjusted antialiasing while maintaining 128-bit colour precision (i.e., 32 bits per channel) throughout the rendering pipeline. Particulars of the algorithm, however, are not readily available.
[1] Akenine-Möller, Tomas and Eric Haines, Real-Time Rendering 2nd. Ed.,
A.K. Peters Ltd, 2002
[2] Blinn, Jim, "Return of the Jaggy", IEEE Computer Graphics and
Applications, IEEE Inc., 9(2):82-89, March 1989
[3] Blinn, Jim, "Dirty Pixels", IEEE Computer Graphics and
Applications, IEEE Inc., 9(4):100-105, July 1989
[4] Bresenham, J.E., "Algorithm for Computer Control of a Digital
Plotter," IBM Systems Journal, 4(1):25-30, 1965
[5] Bresenham, J.E., "Run Length Slice Algorithm for Incremental Lines,"
undemental Algorithms for Computer Graphics, R.A. Earnshaw, ed.,
Springer-Verlag, New York, 1985
[6] Carpenter, Loren, "The A-buffer, an antialiased hidden surface method,"
Proceedings of the 11th annual conference on Computer graphics and
interactive techniques, p.103-108, January 1984
[7] Foley, James D., Andries van Dam, Steven K. Feiner, and John F. Hughes,
Computer graphics: principles and practice (2nd ed.), Addison-Wesley
Longman Publishing Co., Inc., Boston, MA, 1990
[8] Gill, G.W., "N-Step Incremental Straight-Line Algorithms," IEEE
Computer Graphics and Applications, 14(3):66-72, May 1994
[9] nVidia Corporation, "nVidia Accuview Technology: High-Resolution
Antialiasing Subsystem," Technical Brief, 2002
[10] Pitteway, M.L.V., "Algorithm for Drawing Ellipses or Hyperbolae with
a Digital Plotter," Computer Journal, 10(3):282-289, November 1967
[11] Proakis, John G., and Dimitris G. Manolakis, Digital Signal Processing:
Principles, Algorithms, and Applications, Third Edition, Macmillian
Publishing Co., 1995
[12] Rokne, J.G., B. Wyvill, and X. Wu, "Fast Line Scan-Conversion," ACM
Transactions on Graphics, 9(4):376-388, October 1990
[13] Van Aken, J.R., and M. Novak, "Curve-Drawing Algorithms for Raster
Displays," ACM Transactions on Graphics, 4(2):147-169, April 1985
2002.12.11
Display hardware is optimised to process and draw triangles. A surface tesselated into these simple shapes before display. For years computer graphicists have devised techniques to tesselate a parametric surface [18, 19, 22, 23, 25, 26]. Detailed below are three evaluation methods that were developed before the advent of more elegant solutions and alternate surface descriptions.
Bézier surfaces have been around for a very long time [15, 16, 17]. The mathematics are well-established and often discussed with exhaustive detail [21]. Evaluating these surfaces can be a labourious task. Fortunately, we can use another very old concept to help us evaluate the surface very quickly and rather efficiently.
Suppose f(t) represents a function that is differentiable in an interval containing t. The forward difference Df(t) of the function f(t) is
![]()
for k > 0. By moving some terms about, we get
![]()
As an iterative expression,
![]()
where f is evaluated at equal intervals of size k. Evaluating successive function values using the forward difference(s) is known as forward differencing. Notice the above equation contains only one operator: addition. The psuedocode to evaluate a function of one variable is
compute initial conditions f, Df, D2f ... Dnf where t = 0, k > 0 loop from 0 to 1 display f f = f + Df Df = Df + D2f . . . Dn-1f = Dn-1f + Dnf done
EXAMPLE: A quadratic function f(t) and its differences are
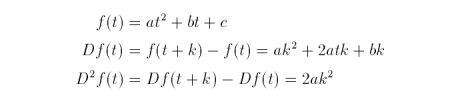
The second difference is a constant, so further differences are not necessary. At initial conditions t = 0 and k > 0.1
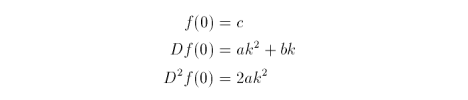
Written in matrix form we have
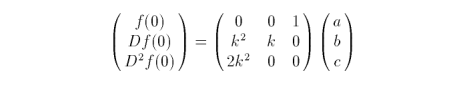
Now, let's see how we can extend this clever logic to evaluate a Bézier surface.
To keep things simple, there are a pair of assumptions to be made. First, the scope of this discussion will only cover biquadratic surfaces. There are enough complications with higher-order surfaces that warrant many long pages of exposition and complex formulae. Second, we will confine our evaluation to spatial coordinates only. Including details such as texture coordinates and normals will simply distract the focus of this section, namely, how forward differencing can be used to evaulate a bivariate function.
The equation for a biquadratic Bézier surface is
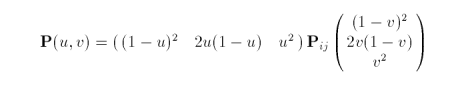
as derived from the general form
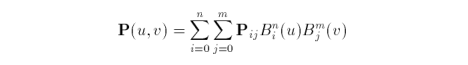
for m = 2 and n = 2. Variables u and v vary in the range from zero to one. The control net is
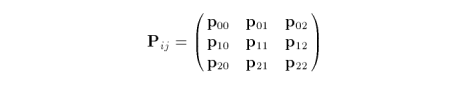
Each element in the matrix is a vector of three components (x, y, z). The blending functions, also known as Bernstein polynomials, are
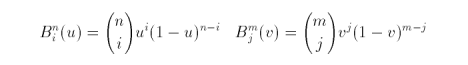

The surface P(u,v) can be thought of as the nesting of one set of curves within another. This visualisation is key in our basic algorithm to evaluate the surface. If we hold one variable constant and simply iterate the other variable from zero to one, our evaluation of the surface is just tracing out a set of quadratic curves. To simplify our algorithm, let's assume that we are sweeping some curve q along curve r where the length and profile of all curves are the same. What we get is a square patch with the same curvature in both axial directions. High-order surfaces such as bicubic, biquartic and biquintic can yield far more interesting patches. The cost, however, is the complexity in evaluation.
For our pair of quadratic Bézier curves q and r
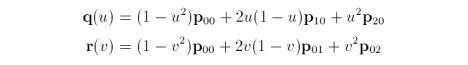
If we collect, say, all u terms we can rewrite q as the summation
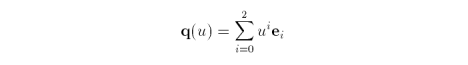
where e are the points that arise when we collect terms. So, q and its differences are
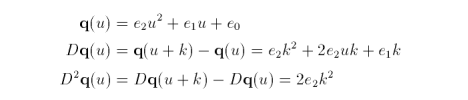
where
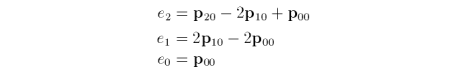
The second difference is a constant, so further differences are not necessary. At initial conditions u = 0 and k > 0.
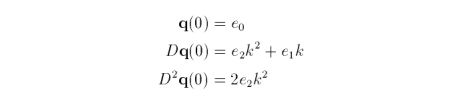
Written in matrix form we have
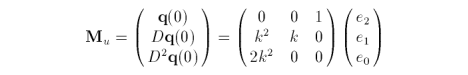
Given our simplifications, the initial conditions of the differences for curves q and r are similar. The forward differences for the biquadratic Bézier surface is
![]()
where, for k = 0.1, the coefficient matrices are
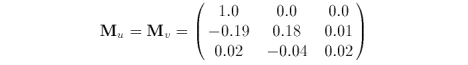
The first row of D is the forward differences along constant v. The second and third rows are the corresponding forward differences for the first row elements. A full implementation to evaluate the surface is provided in section 2.1 Source Code.
The previous section described the differencing scheme where successive values of a function are computed as the parameter(s) vary from zero to one. This iterative method is simple and efficient. If we wish to compute values of a function through subdivision, then central differencing is an option [18]. In this scheme, the point p(t) is computed from known values of p(t - k) and p(t + k) for k > 0. A full treatment of this method is available in several forms [18, 20].
Both forward and central differencing schemes sample the function at uniformly spaced intervals. To provide better accuracy where needed and to avoid unnecessary computations, its best to have the intervals vary depending on several key conditions. Adaptive differencing describes those schemes where the sampling occurs at optimal places along the function [24].
As paraphrased from the GNU General Public License "the following instances of program code are distributed in the hope that it will be useful, but without any warranty; without even the implied warranty of merchantability or fitness for a particular purpose." Please do not hesitate to notify me of any errors in logic and/or semantics.
It is very important to realise, again, that the following evaluator code assumes the curves along constant u and constant v have the same length and curvature profile. Make certain the control net P is defined accordingly. This restriction greatly simplifies the implementation but, in practice, an evalutor must be robust enough to handle any valid control net.
Each point of the tessellated surface is stored in an associative container indexed by an integer. You can, as a result, easily form triangle strip sequences as necessary.
// ----------------------------------------------------------
// Surface.h (for biquadratic surfaces that are uniformly
// sampled in both axial directions)
// ----------------------------------------------------------
#ifndef __SURFACE_H__
#define __SURFACE_H__
#include <iostream>
#include <map>
using namespace std;
typedef struct {
double x, y, z;
} Point;
class Surface
{
public:
Surface(Point [3][3]);
~Surface();
void draw(int);
map<int, Point> getPoints(void);
private:
void init(double);
void plot(double, double, double, int);
double Mu[3][3], Mvt[3][3];
Point D[3][3], P[3][3];
map<int, Point> surfacePoint;
};
inline map<int, Point> Surface::getPoints()
{
return surfacePoint;
}
#endif // __SURFACE_H__
// ----------------------------------------------------------
// Surface.cpp (for biquadratic surfaces that are uniformly
// sampled in both axial directions)
// ----------------------------------------------------------
// The following evaluator code assumes the curves along
// constant 'u' and constant 'v' have the same length and
// curvature profile. Make certain the control net 'P'
// is defined accordingly. This restriction greatly
// simplifies the implementation but, in practice, an
// evalutor must be robust enough to handle any valid
// control net.
#include "surface.h"
Surface::Surface(Point c[][3])
{
int i, j;
for (i=0; i<3; ++i) {
for (j=0; j<3; ++j) {
P[i][j].x = c[i][j].x;
P[i][j].y = c[i][j].y;
P[i][j].z = c[i][j].z;
}
}
surfacePoint.clear();
}
Surface::~Surface() { }
void Surface::draw(int steps)
{
int n;
double k;
double u, v;
double x, y, z;
double dz;
if (steps < 1) return;
k = 1.0 / (double)steps;
init(k);
n = 0;
dz = D[0][1].z;
for (v=0.0; v<=1.0; v+=k) {
x = D[0][0].x;
y = D[0][0].y;
z = D[0][0].z;
for (u=0.0; u<=1.0; u+=k) {
plot(x, y, z, n);
x += D[0][1].x; D[0][1].x += D[0][2].x;
y += D[0][1].y; D[0][1].y += D[0][2].y;
z += D[0][1].z; D[0][1].z += D[0][2].z;
++n;
}
// update first row of D. some of these calculations
// are redundant but are included here for completeness
//
D[0][0].x += D[1][0].x;
D[0][0].y += D[1][0].y;
D[0][0].z += D[1][0].z;
D[0][1].z = dz;
D[0][1].x += D[1][1].x;
D[0][1].y += D[1][1].y;
D[0][1].z += D[1][1].z;
D[0][2].x += D[1][2].x;
D[0][2].y += D[1][2].y;
D[0][2].z += D[1][2].z;
// update second row of D. some of these calculations
// are redundant but are included here for completeness
//
D[1][0].x += D[2][0].x;
D[1][0].y += D[2][0].y;
D[1][0].z += D[2][0].z;
D[1][1].x += D[2][1].x;
D[1][1].y += D[2][1].y;
D[1][1].z += D[2][1].z;
D[1][2].x += D[2][2].x;
D[1][2].y += D[2][2].y;
D[1][2].z += D[2][2].z;
}
}
void Surface::init(double k)
{
int i, j, k_;
double sumX, sumY, sumZ;
Point t[3][3];
Mu[0][0] = Mvt[0][0] = 1.0;
Mu[0][1] = Mvt[1][0] = 0.0;
Mu[0][2] = Mvt[2][0] = 0.0;
Mu[1][0] = Mvt[0][1] = k*k - 2*k;
Mu[1][1] = Mvt[1][1] = 2*k*(1 - k);
Mu[1][2] = Mvt[2][1] = k*k;
Mu[2][0] = Mvt[0][2] = 2*k*k;
Mu[2][1] = Mvt[1][2] = -4*k*k;
Mu[2][2] = Mvt[2][2] = 2*k*k;
// t = Mu * P
//
for (i=0; i<3; ++i) {
for (j=0; j<3; ++j) {
t[i][j].x = 0.0;
t[i][j].y = 0.0;
t[i][j].z = 0.0;
}
}
for (i=0; i<3; ++i) {
for (j=0; j<3; ++j) {
sumX = 0.0;
sumY = 0.0;
sumZ = 0.0;
for (k_=0; k_<3; ++k_) {
sumX += Mu[i][k_] * P[k_][j].y;
sumY += Mu[i][k_] * P[k_][j].y;
sumZ += Mu[i][k_] * P[k_][j].z;
}
t[i][j].x += sumX;
t[i][j].y += sumY;
t[i][j].z += sumZ;
}
}
// D = t * Mvt
//
for (i=0; i<3; ++i) {
for (j=0; j<3; ++j) {
sumX = 0.0;
sumY = 0.0;
sumZ = 0.0;
for (k_=0; k_<3; ++k_) {
sumX += t[i][k_].x * Mvt[k_][j];
sumY += t[i][k_].y * Mvt[k_][j];
sumZ += t[i][k_].z * Mvt[k_][j];
}
D[i][j].x += sumX;
D[i][j].y += sumY;
D[i][j].z += sumZ;
}
}
}
void Surface::plot(double x, double y, double z, int n)
{
Point p;
p.x = x;
p.y = y;
p.z = z;
surfacePoint[n] = p;
}
[14] Bernstein, S., Démonstration du théorème de
Weierstrass fondeé sur le calcul des probabilités.
Harkov Soobs. Matem ob-va, 13:1-2, 1912
[15] Bézier, P., Procédé de définition numérique des
courbes et surfaces non mathématiques. Automatisme, XIII(5):189-196,
1968
[16] Bézier, P., Mathematical and Practical Possibilities of UNISURF. In
R. Barnhill and R. Riesenfeld, editors, Computer Aided Geometric Design,
Academic Press, 127-152, 1974
[17] Bézier, P., Essay de définition numérique des courbes et
des surfaces expérimentales. Ph.D. dissertation, University of Paris VI,
France, 1977
[18] Catmull, E.E., A Subdivision Algorithm for Computer Display of Curved
Surfaces, Ph.D. Thesis, University of Utah, USA, December 1974
[19] Clark, James H., A Fast Algorithm to Render Parametric Surfaces,
Computer Graphics, SIGGRAPH 1979 Proceedings, 13(4):7-12
[20] DeLoura, Mark A., An In-depth Look at Bicubic Bézier Surfaces,
Gamasutra, CMP Media LLC, October 27, 1999
[21] Farin, G., Curves and Surfaces for Computer-Aided Geometric Design: A
Practical Guide, Fourth Edition, Academic Press, San Diego, 1997
[22] Klassen, R.V., Integer Forward Differencing of Cubic Polynomials:
Analysis and Algorithms, ACM Transactions on Graphics, 10(2):152-181,
April 1991
[23] Klassen, R.V., Exact Integer Hybrid Subdivision and Forward
Differencing of Cubics, ACM Transactions on Graphics, 13(3):240-255,
July 1994
[24] Lien, Sheue-Ling, Michael Shantz and Vaughna Pratt, Adaptive
Forward Differencing for Rendering Curves and Surfaces, Computer
Graphics SIGGRAPH 1987 Proceedings, 21(4):111-118
[25] Rappoport, A., Renderings Curves and Surfaces with Hybrid
Subdivision and Forward Differencing, ACM Transcations on Graphics,
10(4):323-341, October 1991
[26] Rayner, Mike, GDC 2002: Dynamic Level of Detail Terrain Rendering
with Bézier Patches, Gamasutra, March 21, 2002