2003.03.23
Almost three decades ago, Chaikin introduced an ingenious method for generating curves [68]. The algorithm was a corner cutting or refinement scheme that produced a smooth curve from a given control polygon. In the following years, many subdivision schemes for modeling smooth objects have been developed based on Chaikin's pioneering endeavour. First among these schemes were techniques developed Catmull and Clark [67, 69].
An algorithm that subdivides a surface applies some basic rules to vertices, edges and faces. The rule to generate a new vertex is called a vertex mask. Likewise, the rules to generate new edges and new faces are called, respectively, edge masks and face masks. Chaikin's scheme of corner cutting applies a vertex mask to each pair of vertices to establish two new vertices.
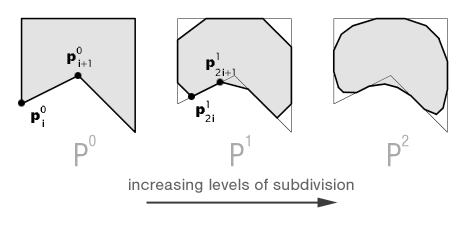
The leftmost shape is known as the initial control mesh P0 where the superscript denotes its level of subdivision. As we subdivide, the shape becomes more refined. Continuing this process to some predefined limit yields a shape called the limit surface. With Chaikin's scheme the next control mesh has double the number of vertices as the mesh before it. The vertex mask, in this case, is simply
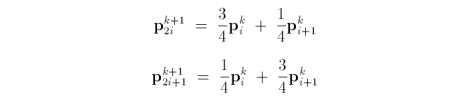
where k is the subdivision level for the i-th vertex p in control mesh Pk. In other words, each new vertex is the weighted sum of two vertices in the previous subdivision level. Chaikin's scheme is an approximating subdivision technique because a given mesh does not retain vertices from the previous subdivision step. The scheme is stationary because it uses the same masks at every subdivision step, and the scheme is also uniform because it uses the same masks for every vertex.
A well-known scheme that is stationary, uniform and polygon-based is Catmull-Clark subdivision. The method is approximating, rather than interpolating, and has been applied in commerical productions by Pixar Animation Studios. The actual subdivision process is simple, but the management of the resultant dataset can be complex.
Consider the vertex vk surrounded by n edge points ei where i = 0 ... n - 1
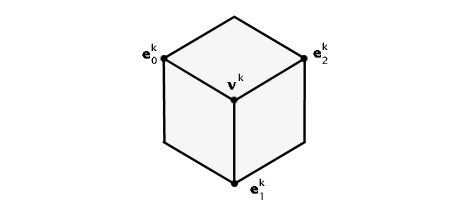
For each face adjacent to vk we compute new face points fk+1. Each new face point is the average of all vertices that define the face.
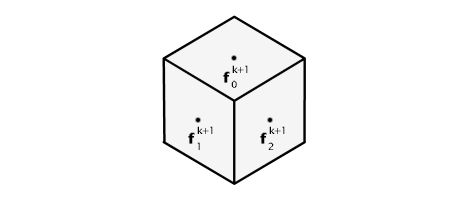
For each edge incident to vk we compute new edge points ek+1. Each new edge point is the average of four points: the two endpoints that define the edge and the two new face points of the faces adjacent to the edge.
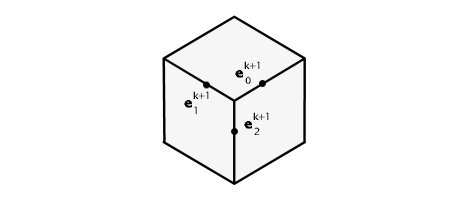
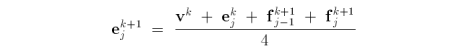
where the subscripts are taken to be modulo n [73]. Next, we compute the new vertex
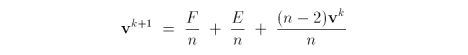
where F is the average of the new face points adjacent to vk, E is the average of the edge points incident to the old vertex and n is the number of edges incident to the old vertex [75].
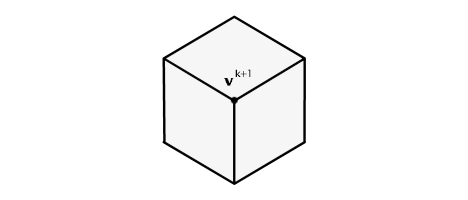
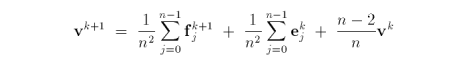
To reconstruct the mesh, using these new points, we first connect each new face point to the new edge points, and then connect the new vertex to the new edge points.
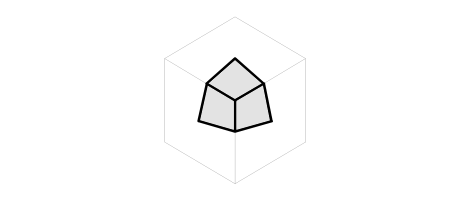
Note that each new face of the refined mesh has four edges.
The subdivision rules, thus far, yield smooth continuous surfaces. To produce sharp edges anywhere along the surface, we apply a different set of masks. A new edge point along a sharp edge is the average of the two adjacent vertices. The new vertex of a point with more than two incident sharp edges is simply
![]()
The new vertex of a point with exactly two incident sharp edges is
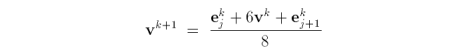
The vertex mask for a point with less than two incident sharp edges is either the same mask used in the general case
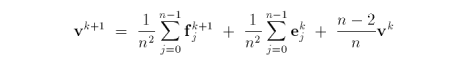
or the appropriate mask described in section 7.0.2.4 Extraordinary Vertices.
A quadrilateral mesh is a mesh consisting of four-sided polygons (faces) throughout the entire surface. This mesh is regular if all vertices have a valence of four. In such a case, the subdivision rules can be expressed in a simplified form. To calculate a new point we apply a set of fixed weights to the appropriate set of vertices.
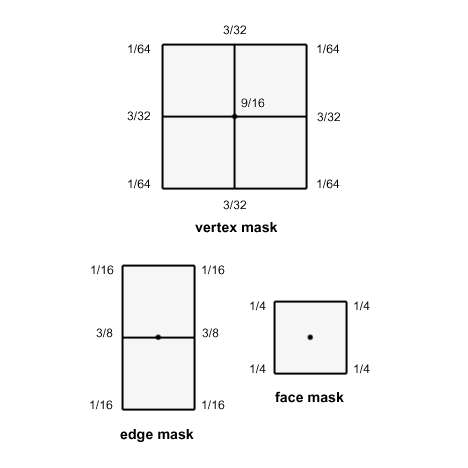
An extraordinary vertex, in a quadrilateral mesh, has a valence not equal to four. The vertex mask applied at the interior of the mesh, for these points, is
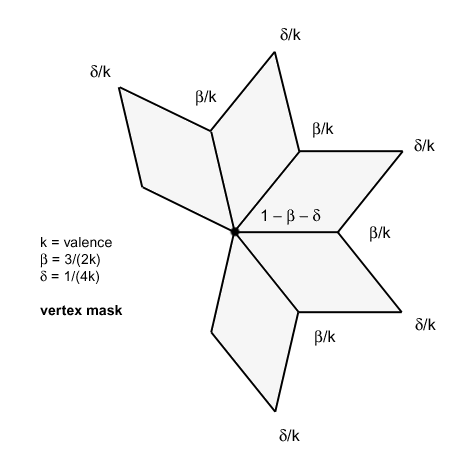
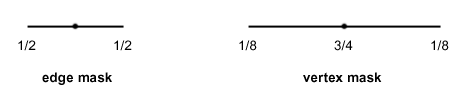
Points that define the boundary of an open mesh are also extraordinary. The standard subdivision rules applied to a boundary are
Digital artists often model complex three-dimensional objects using more than one surface patch. The boundaries of these patches are known as crease edges. Joining patches along their crease edges may introduce new surface features. Biermann et. al., developed an improved set of subdivision rules, for edges, to ensure smoothness near these features [65].
When a crease edge blends smoothly into a surface we have a dart vertex along the crease. This is the ideal case of a composite surface: there is parametric continuity (identical first and possibly second derivates) and geometric continuity (no gaps) along the interface of the patches. If exactly two crease edges are joined smoothly, they are incident to a crease vertex. The edge mask that includes a dart or crease vertex assigns a variable weight to the points that define the edge. A corner vertex connects two or more crease edges. The mask we use to compute a new edge point near a corner vertex depends on how the surface approaches the corner.
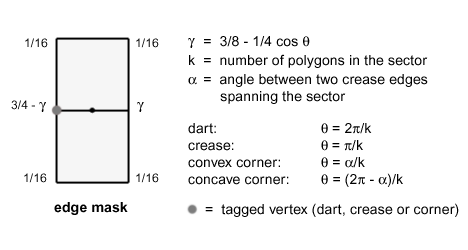
A sector is an area bounded by at least one crease edge. If tagged vertex v is a dart, k is the number of all polygons adjacent to the vertex. If v is a crease or corner, k is the number of polygons adjacent to the vertex in the sector only. The angle between two crease edges is measured in radians.
There are many ways in which one can implement Catmull-Clark subdivision. We chose a simplistic and non-production quality implementation. The most direct use of the code in 7.2 Source Code is to instantiate a CatmullClark object, load the surface description and invoke the draw method as follows:
#include "catmullClark.h"
#include "quadTreeRoot.h"
int main(int argc, char *argv[])
{
CatmullClark *cc;
cc = new CatmullClark(new QuadTreeRoot);
if (argc > 1 && cc->load(argv[argc-1])) {
cc->draw(1); // draw limit surface P^1
}
delete cc;
return 0;
}
All source files are available for download. Some results from applying the code in section 7.2 Source Code are shown below where the base mesh is rendered in grey and the limit surface in black.
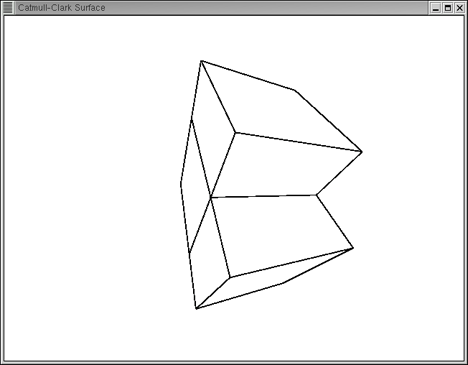
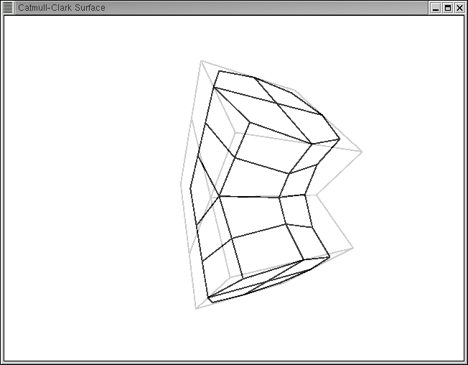
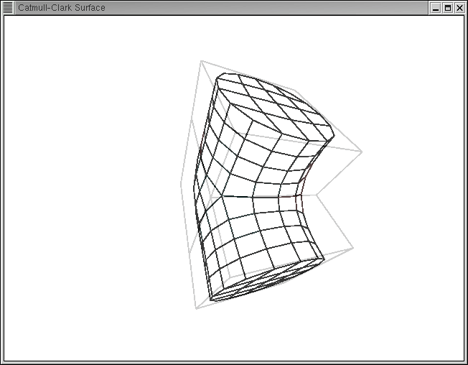
A vertex has several attributes including its spatial coordinates in Cartesian space, its RGBA colour and the normal vector. These vertices are stored in a vector and are indexed via positive integers in range from 0 to N. Polygons in our model consist of four vertices. These polygons are also stored in a vector and are indexed via positive integers in range from 0 to M.
At each subdivision level, the surface is described by a set of polygons. Each polygon P of the base mesh is stored at the root of a single quadtree Q. A cube, for example, consists of six quads and therefore we need to maintain six quadtrees. Subsequent subdivisions of the base mesh polygon P are stored at the child nodes of Q.
Catmull-Clark subdivision quadrisects all polygons of a quad mesh. It is therefore a natural inclination to use quadtrees in this context to store the elements of the limit surface(s). As with any topic in computer graphics, however, one can opt for any other data management scheme. To provide a measure of flexibilty in our code, we used the strategy design pattern in the event we wish to test alternate schemes to manage our polygons [72]. As noted by Gemma, et. al., the strategy design pattern has several consequences. On the plus side, by encapsulating our algorithms we can very easily modify any algorithm independently of its context. We also provide the client (in this case the CatmullClark class) the opportunity to choose among a set of strategies with varying run-time performance and memory space trade-offs. On the negative side, there is some communication overhead and excess amount of objects floating about. Overall, we believe the benefits far outweigh the drawbacks.
As paraphrased from the GNU General Public License "the following instances of program code are distributed in the hope that it will be useful, but without any warranty; without even the implied warranty of merchantability or fitness for a particular purpose." Please do not hesitate to notify me of any errors in logic and/or semantics.
All source files, including a sample surface description, are available for download.
// ----------------------------------------------------------
// polygon.h
// ----------------------------------------------------------
#ifndef __POLYGON_H__
#define __POLYGON_H__
class Polygon
{
public:
Polygon();
~Polygon();
int v[4]; // vertex IDs
int n[4]; // neighbour IDs
int id; // id of this polygon
int pid; // id of the base mesh polygon
void clear(void);
};
#endif // __POLYGON_H__
// ----------------------------------------------------------
// polygon.cpp
// ----------------------------------------------------------
#include "polygon.h"
Polygon::Polygon()
{
clear();
}
Polygon::~Polygon() { }
void Polygon::clear()
{
v[0] = 0;
v[1] = 0;
v[2] = 0;
v[3] = 0;
n[0] = 0;
n[1] = 0;
n[2] = 0;
n[3] = 0;
id = 0;
pid = 0;
}
// ----------------------------------------------------------
// vertex.h
// ----------------------------------------------------------
#ifndef __VERTEX_H__
#define __VERTEX_H__
class Vertex
{
public:
Vertex() {};
~Vertex() {};
// enumeration of vertex types
//
enum { Regular = 0, Dart, Crease, ConvexCorner,
ConcaveCorner };
double p[3]; // Cartesian coordinates
double c[4]; // RGBA colour
double n[3]; // normal
int id; // id of this vertex
int tag; // type of vertex
int subLevel; // subdivision level at which this vertex
// occupies
int pid; // id of the base mesh polygon
void clear(void);
};
#endif // __VERTEX_H__
// ----------------------------------------------------------
// vertex.cpp
// ----------------------------------------------------------
#include "vertex.h"
Vertex::Vertex()
{
clear();
}
Vertex::~Vertex() { }
void Vertex::clear()
{
p[0] = 0.0;
p[1] = 0.0;
p[2] = 0.0;
c[0] = 0.0;
c[1] = 0.0;
c[2] = 0.0;
c[3] = 0.0;
n[0] = 0.0;
n[1] = 0.0;
n[2] = 0.0;
id = 0;
tag = Vertex::Regular;
subLevel = 0;
pid = 0;
}
// ----------------------------------------------------------
// kdTreeRoot.h (abstract class for all strategies)
// ----------------------------------------------------------
#ifndef __KDTREE_ROOT_H__
#define __KDTREE_ROOT_H__
#include "vertex.h"
#include "polygon.h"
#include <vector>
class KDTreeRoot
{
public:
virtual void add(int, Polygon *) = 0;
virtual void traverse(int) = 0;
virtual void create(void) = 0;
virtual void augmentVertexPool(Vertex *) = 0;
virtual void augmentPolygonPool(Polygon *) = 0;
virtual vector<Vertex*> getVertexPool(void) = 0;
virtual vector<Polygon*> getPolygonPool(void) = 0;
virtual void setVertexPool(vector<Vertex*>) = 0;
virtual void setPolygonPool(vector<Polygon*>) = 0;
virtual int getMaxSubLevel(void) = 0;
virtual void setMaxSubLevel(int) = 0;
~KDTreeRoot(); // should be virutal ;-)
protected:
vector<Vertex*> vertexPool; // vertices of the surface
vector<Polygon*> polygonPool; // polygons of the surface
int maxSubLevel;
KDTreeRoot();
};
#endif // __KDTREE_ROOT_H__
// ----------------------------------------------------------
// kdTreeRoot.cpp (abstract class for all strategies)
// ----------------------------------------------------------
#include "kdTreeRoot.h"
KDTreeRoot::KDTreeRoot()
{
vertexPool.clear();
polygonPool.clear();
}
KDTreeRoot::~KDTreeRoot()
{
int i, n;
n = vertexPool.size();
for (i=0; i<n; ++i) delete vertexPool[i];
n = polygonPool.size();
for (i=0; i<n; ++i) delete polygonPool[i];
}
// ----------------------------------------------------------
// quadTree.h
// ----------------------------------------------------------
#ifndef __QUAD_TREE_H__
#define __QUAD_TREE_H__
#include <iostream>
#include "vertex.h"
#include "polygon.h"
class QuadTree
{
public:
QuadTree();
~QuadTree();
void setParent(QuadTree *);
void setChild(int, QuadTree *);
void setPoly(Polygon *);
void setSubdivisionLevel(int);
QuadTree* getParent(void);
QuadTree* getChild(int);
Polygon* getPoly(void);
int getSubdivisionLevel(void);
private:
QuadTree *p; // parent
QuadTree *c[4]; // children
Polygon *polygon; // a portion of the surface
int subLevel; // subdivision level at which this
// tree node exists
};
inline void QuadTree::setParent(QuadTree *parent)
{
p = parent;
}
inline void QuadTree::setChild(int i, QuadTree *child)
{
c[i] = child;
}
inline void QuadTree::setSubdivisionLevel(int i)
{
subLevel = i;
}
inline QuadTree* QuadTree::getParent()
{
return p;
}
inline QuadTree* QuadTree::getChild(int i)
{
return c[i];
}
inline Polygon* QuadTree::getPoly()
{
return polygon;
}
inline int QuadTree::getSubdivisionLevel()
{
return subLevel;
}
#endif // __QUAD_TREE_H__
// ----------------------------------------------------------
// quadTree.cpp
// ----------------------------------------------------------
#include "quadTree.h"
QuadTree::QuadTree()
{
int i;
for (i=0; i<4; ++i) {
c[i] = NULL;
}
p = NULL;
subLevel = 0;
polygon = new Polygon();
}
QuadTree::~QuadTree()
{
int i;
for (i=0; i<4; ++i) {
if (c[i] != NULL) delete c[i];
}
delete polygon;
}
void QuadTree::setPoly(Polygon *p)
{
polygon->v[0] = p->v[0];
polygon->v[1] = p->v[1];
polygon->v[2] = p->v[2];
polygon->v[3] = p->v[3];
polygon->n[0] = (p->n[0] < 0) ? -p->n[0] : p->n[0];
polygon->n[1] = (p->n[1] < 0) ? -p->n[1] : p->n[1];
polygon->n[2] = (p->n[2] < 0) ? -p->n[2] : p->n[2];
polygon->n[3] = (p->n[3] < 0) ? -p->n[3] : p->n[3];
polygon->id = p->id;
polygon->pid = p->pid;
}
// ----------------------------------------------------------
// quadTreeRoot.h
// ----------------------------------------------------------
#ifndef __QUAD_TREE_ROOT_H__
#define __QUAD_TREE_ROOT_H__
#include "quadTree.h"
#include "kdTreeRoot.h"
#include <queue>
class QuadTreeRoot : public KDTreeRoot
{
public:
QuadTreeRoot();
~QuadTreeRoot(); // should be virtual ;-)
virtual void add(int, Polygon *);
virtual void traverse(int);
virtual void create(void);
virtual void augmentVertexPool(Vertex *);
virtual void augmentPolygonPool(Polygon *);
virtual int getMaxSubLevel(void);
virtual void setMaxSubLevel(int);
vector<Vertex*> getVertexPool(void);
vector<Polygon*> getPolygonPool(void);
void setVertexPool(vector<Vertex*>);
void setPolygonPool(vector<Polygon*>);
private:
void deepAdd(int *, int, int, Polygon *, QuadTree *);
void createForest(QuadTreeRoot *, int, int);
void findForest(QuadTreeRoot *, QuadTreeRoot **, int);
void visitForest(int, QuadTreeRoot *);
void visitNode(int, QuadTree *);
QuadTreeRoot *n[4]; // neighbours
QuadTree *root; // actual tree
int id; // id of this forest node
};
inline void QuadTreeRoot::augmentVertexPool(Vertex *v)
{
vertexPool.push_back(v);
}
inline void QuadTreeRoot::augmentPolygonPool(Polygon *p)
{
polygonPool.push_back(p);
}
inline
vector<Vertex*> QuadTreeRoot::getVertexPool()
{
return vertexPool;
}
inline
vector<Polygon*> QuadTreeRoot::getPolygonPool()
{
return polygonPool;
}
inline
void QuadTreeRoot::setVertexPool(vector<Vertex*> pool)
{
vertexPool = pool;
}
inline
void QuadTreeRoot::setPolygonPool(vector<Polygon*> pool)
{
polygonPool = pool;
}
inline int QuadTreeRoot::getMaxSubLevel()
{
return maxSubLevel;
}
inline void QuadTreeRoot::setMaxSubLevel(int s)
{
maxSubLevel = s;
}
#endif // __QUAD_TREE_ROOT_H__
// ----------------------------------------------------------
// quadTreeRoot.cpp
// ----------------------------------------------------------
#include "quadTreeRoot.h"
QuadTreeRoot::QuadTreeRoot()
{
int i;
root = new QuadTree();
for (i=0; i<4; ++i) {
n[i] = NULL;
}
maxSubLevel = 0;
id = 0;
}
QuadTreeRoot::~QuadTreeRoot()
{
int i;
delete root;
for (i=0; i<4; ++i) {
if (n[i] != NULL) delete n[i];
}
}
void QuadTreeRoot::add(int subLevel, Polygon *p)
{
int i, done;
QuadTreeRoot *target;
QuadTree *q, *qn;
queue<QuadTree*> qt;
if (subLevel < 0) return;
target = NULL;
findForest(this, &target, p->pid);
if (target != NULL) {
q = target->root;
// add polygon to appropriate child
// of the forest root
//
if (subLevel < 2) {
for (i=0; i<4; ++i) {
if (q->getChild(i) == NULL) {
qn = new QuadTree();
qn->setSubdivisionLevel(subLevel);
qn->setPoly(p);
qn->setParent(q);
q->setChild(i, qn);
break;
}
}
} else {
done = 0;
deepAdd(&done, subLevel-1, 0, p, q);
}
}
}
void
QuadTreeRoot::deepAdd(int *done, int subLevel, int child,
Polygon *p, QuadTree *q)
{
int i;
QuadTree *qn, *parent;
// iterate through quadtree to add polygon
// to appropriate child
//
if (*done || q == NULL) return;
if (q->getSubdivisionLevel() == subLevel) {
for (i=0; i<4 && !(*done); ++i) {
if (q->getChild(i) == NULL) {
qn = new QuadTree();
qn->setSubdivisionLevel(subLevel+1);
qn->setPoly(p);
qn->setParent(q);
q->setChild(i, qn);
*done = 1;
}
}
if ( !(*done) ) {
// traverse to sibling
//
if (child < 3) {
++child;
parent = q->getParent();
deepAdd(done, subLevel, child, p,
parent->getChild(child));
} else {
// logic flow reaches here for degenerate cases
//
}
}
} else {
// traverse to children
//
deepAdd(done, subLevel, 0, p, q->getChild(0));
deepAdd(done, subLevel, 1, p, q->getChild(1));
deepAdd(done, subLevel, 2, p, q->getChild(2));
deepAdd(done, subLevel, 3, p, q->getChild(3));
}
}
void QuadTreeRoot::create()
{
int polyID;
polyID = polygonPool[0]->id;
if (polyID < 1) return;
createForest(this, 0, polyID);
}
void QuadTreeRoot::createForest(QuadTreeRoot *forest,
int sourcePolyID,
int polyID)
{
int oldSourcePolyID, isLeaf, i;
QuadTree *qt;
Polygon *p;
if (forest == NULL) return;
isLeaf = 0;
// tag this forest as a leaf if polyID is negative
//
if (polyID < 0) {
isLeaf = 1;
polyID = -polyID;
}
oldSourcePolyID = sourcePolyID;
sourcePolyID = polyID;
// store polygon in quadtree
//
qt = forest->root;
p = polygonPool[polyID-1];
qt->setPoly(p);
qt->setSubdivisionLevel(0);
// tag this forest with the id of the polygon
// belonging to the base mesh
//
forest->id = p->id;
// terminate forest creation at leaf node
//
if (isLeaf) return;
// populate other forests
//
for (i=0; i<4; ++i) {
if (p->n[i] > 0 &&
p->n[i] != polyID &&
p->n[i] != oldSourcePolyID) {
forest->n[i] = new QuadTreeRoot();
createForest(forest->n[i], sourcePolyID, p->n[i]);
}
}
}
void QuadTreeRoot::findForest(QuadTreeRoot *forest,
QuadTreeRoot **target,
int polyID)
{
if (forest == NULL || *target != NULL) return;
if (forest->id == polyID) {
*target = forest;
} else {
findForest(forest->n[0], target, polyID);
findForest(forest->n[1], target, polyID);
findForest(forest->n[2], target, polyID);
findForest(forest->n[3], target, polyID);
}
}
void QuadTreeRoot::traverse(int subLevel)
{
visitForest(subLevel, this);
}
void QuadTreeRoot::visitForest(int subLevel,
QuadTreeRoot *forest)
{
if (forest == NULL) return;
visitNode(subLevel, forest->root);
visitForest(subLevel, forest->n[0]);
visitForest(subLevel, forest->n[1]);
visitForest(subLevel, forest->n[2]);
visitForest(subLevel, forest->n[3]);
}
void QuadTreeRoot::visitNode(int subLevel, QuadTree *qt)
{
QuadTree *t;
queue<QuadTree*> q;
if (subLevel < 0 || qt == NULL) return;
q.push(qt);
while (q.empty() == false) {
t = q.front();
q.pop();
if (t->getSubdivisionLevel() > subLevel) break;
if (t->getSubdivisionLevel() == subLevel) {
// invoke method something like
// Rasteriser::drawPoly(t->getPoly());
//
}
if (t->getChild(0) != NULL) q.push(t->getChild(0));
if (t->getChild(1) != NULL) q.push(t->getChild(1));
if (t->getChild(2) != NULL) q.push(t->getChild(2));
if (t->getChild(3) != NULL) q.push(t->getChild(3));
}
}
// ----------------------------------------------------------
// parser.h (a very basic text parser)
// ----------------------------------------------------------
#ifndef __PARSER_H__
#define __PARSER_H__
#include <string>
#include <iostream>
#include <algorithm>
#include <vector>
class Parser
{
public:
Parser();
~Parser();
int split(char *, string);
int split(char *, char);
int split(string, char);
int split(string, string);
vector<string> getVector(void);
private:
vector<string> target;
};
inline vector<string> Parser::getVector()
{
return target;
}
#endif // __PARSER_H__
// ----------------------------------------------------------
// parser.cpp (a very basic text parser)
// ----------------------------------------------------------
#include "parser.h"
Parser::Parser() { }
Parser::~Parser() { }
int Parser::split(char *source, string fieldSep)
{
string s(source);
return split(s, fieldSep);
}
int Parser::split(char *source, char fieldSep)
{
string a(1, fieldSep);
string s(source);
return split(s, a);
}
int Parser::split(string source, char fieldSep)
{
string a(1, fieldSep);
return split(source, a);
}
int Parser::split(string source, string fieldSep)
{
int a;
int b;
int d = source.length();
int e = fieldSep.length();
target.clear();
// check for valid argument(s)
//
if (d < 1 || e < 1) return 0;
// perform split operation
//
a = 0;
while (a < d) {
b = source.find(fieldSep, a);
if (b != string::npos) {
if (b-a > 0) target.push_back(source.substr(a, b-a));
a = b+e;
} else {
if (a > 0) target.push_back(source.substr(a, b-a));
break;
}
}
return target.size();
}
// ----------------------------------------------------------
// catmullClark.h (for quad meshes only)
// ----------------------------------------------------------
#ifndef __CATMULL_CLARK_H__
#define __CATMULL_CLARK_H__
#include <string>
#include <fstream>
#include <map>
#include "kdTreeRoot.h"
#include "parser.h"
class CatmullClark
{
public:
CatmullClark(KDTreeRoot *);
~CatmullClark();
int load(char *);
void draw(int);
private:
void applySubdivisionRules(int);
int findDuplicateVertex(Vertex *);
int findAdjacentFaceID(vector<int>, int, int);
vector<int> faceMask(vector<int>, int);
vector<int> edgeMask(vector<int>, vector<int>,
vector<int>, int, int);
int vertexMask(vector<int>, vector<int>, int, int);
vector<Vertex*> vertexPool; // vertices of the surface
vector<Polygon*> polygonPool; // polygons of the surface
map<int, int> adjacentEdgePoints;
KDTreeRoot *forest; // root of all forests
};
#endif // __CATMULL_CLARK_H__
// ----------------------------------------------------------
// catmullClark.cpp (for quad meshes only)
// ----------------------------------------------------------
#include "catmullClark.h"
CatmullClark::CatmullClark(KDTreeRoot *k)
{
forest = k;
}
CatmullClark::~CatmullClark()
{
delete forest;
adjacentEdgePoints.clear();
}
// returns non-zero on success
//
int CatmullClark::load(char *fileName)
{
int numTokens;
string line;
vector<string> s;
Parser *par;
Polygon *p;
Vertex *v;
ifstream file(fileName);
if (file.is_open() == false) return 0;
par = new Parser;
numTokens = 0;
while (getline(file, line, '\n')) {
numTokens = par->split(line, " ");
if (numTokens > 0) {
s = par->getVector();
switch(line[0]) {
case 'v':
if (s.size() != 13) {
cerr << "Invalid vertex definition in "
<< fileName << endl;
file.close();
delete par;
return 0;
}
v = new Vertex();
// Cartesian coordinates
//
v->p[0] = strtod(s[1].c_str(), NULL);
v->p[1] = strtod(s[2].c_str(), NULL);
v->p[2] = strtod(s[3].c_str(), NULL);
// RGBA colour
//
v->c[0] = strtod(s[4].c_str(), NULL);
v->c[1] = strtod(s[5].c_str(), NULL);
v->c[2] = strtod(s[6].c_str(), NULL);
v->c[3] = strtod(s[7].c_str(), NULL);
// normal
//
v->n[0] = strtod(s[8].c_str(), NULL);
v->n[1] = strtod(s[9].c_str(), NULL);
v->n[2] = strtod(s[10].c_str(), NULL);
// unique identifiers
//
v->id = atoi(s[11].c_str());
v->tag = atoi(s[12].c_str());
if (v->tag < Vertex::Regular ||
v->tag > Vertex::ConcaveCorner) {
v->tag = Vertex::Regular;
}
v->subLevel = 0;
v->pid = v->id;
forest->augmentVertexPool(v);
break;
case 'p':
if (s.size() != 10) {
cerr << "Invalid polygon definition in "
<< fileName << endl;
file.close();
delete par;
return 0;
}
p = new Polygon();
// vertices
//
p->v[0] = atoi(s[1].c_str());
p->v[1] = atoi(s[2].c_str());
p->v[2] = atoi(s[3].c_str());
p->v[3] = atoi(s[4].c_str());
// neighbours
//
p->n[0] = atoi(s[5].c_str());
p->n[1] = atoi(s[6].c_str());
p->n[2] = atoi(s[7].c_str());
p->n[3] = atoi(s[8].c_str());
// unique identifiers
//
p->id = atoi(s[9].c_str());
p->pid = p->id;
forest->augmentPolygonPool(p);
break;
default:
break;
}
}
}
file.close();
delete par;
forest->create();
vertexPool = forest->getVertexPool();
polygonPool = forest->getPolygonPool();
return 1;
}
void CatmullClark::draw(int subLevel)
{
if (subLevel < 0) return;
if (subLevel > forest->getMaxSubLevel()) {
applySubdivisionRules(subLevel);
}
forest->traverse(subLevel);
}
void
CatmullClark::applySubdivisionRules(int s)
{
Vertex *u;
Polygon *p, *g;
vector<int> polyList;
vector<int> vertList;
vector<int> newFacePoints;
vector<int> newEdgePoints;
int newVertexID;
int i, j, k, m, pmax, vmax, fmax;
if (forest->getMaxSubLevel() < s) {
forest->setMaxSubLevel(s);
}
pmax = polygonPool.size();
vmax = vertexPool.size();
adjacentEdgePoints.clear();
for (i=0; i<vmax; ++i) {
// scan through polygonPool to determine which
// edges and faces are incident/adjacent to
// vertex 'i'
//
vertList.clear();
polyList.clear();
for (j=0; j<pmax; ++j) {
p = polygonPool[j];
for (k=0; k<4; ++k) {
u = vertexPool[p->v[k]];
if (p->v[k] == i &&
u->subLevel == s-1) {
vertList.push_back(p->v[(k+1)&3]);
polyList.push_back(p->id);
break;
}
}
}
if (vertList.size() > 1 && polyList.size() > 1) {
// apply all masks to calculate surface points
//
newFacePoints=faceMask(polyList, s);
newEdgePoints=edgeMask(vertList, newFacePoints,
polyList, i, s);
newVertexID=vertexMask(vertList, newFacePoints, i, s);
// add polygon(s) to children
//
fmax = newFacePoints.size();
for (m=0; m<fmax; ++m) {
g = new Polygon();
g->v[0] = newVertexID;
g->v[1] = newEdgePoints[m];
g->v[2] = newFacePoints[m];
g->v[3] = adjacentEdgePoints[g->v[2]];
g->id = polygonPool.size()+1;
g->pid = vertexPool[g->v[2]]->pid;
polygonPool.push_back(g);
forest->add(s, g);
}
}
}
forest->setVertexPool(vertexPool);
forest->setPolygonPool(polygonPool);
}
// returns integer greater than or equal to zero
// on success
//
int CatmullClark::findDuplicateVertex(Vertex *v)
{
Vertex *u;
int i, n;
n = vertexPool.size();
for (i=0; i<n; ++i) {
u = vertexPool[i];
if (u->p[0] == v->p[0] &&
u->p[1] == v->p[1] &&
u->p[2] == v->p[2]) {
return u->id;
}
}
return -1;
}
int CatmullClark::findAdjacentFaceID(vector<int> polyList,
int e0, int e1)
{
Polygon *p;
int i, j, n, prev;
// scan through polyList to locate the
// face point adjacent to edge (e0, e1)
//
n = polyList.size();
for (i=0; i<n; ++i) {
p = polygonPool[polyList[i]-1];
prev = 3;
for (j=0; j<4; ++j) {
if (p->v[j] == e0 && p->v[prev] == e1) {
return i;
}
prev = j;
}
}
return n-1;
}
vector<int> CatmullClark::faceMask(vector<int> polyList,
int subLevel)
{
vector<int> newVertices;
Vertex *v, *nv;
Polygon *p;
int i, j, n, dupID;
newVertices.clear();
n = polyList.size();
for (i=0; i<n; ++i) {
nv = new Vertex();
p = polygonPool[polyList[i]-1];
for (j=0; j<4; ++j) {
v = vertexPool[p->v[j]];
nv->p[0] += v->p[0];
nv->p[1] += v->p[1];
nv->p[2] += v->p[2];
nv->c[0] += v->c[0];
nv->c[1] += v->c[1];
nv->c[2] += v->c[2];
nv->c[3] += v->c[3];
nv->n[0] += v->n[0];
nv->n[1] += v->n[1];
nv->n[2] += v->n[2];
}
nv->p[0] *= 0.25;
nv->p[1] *= 0.25;
nv->p[2] *= 0.25;
nv->c[0] *= 0.25;
nv->c[1] *= 0.25;
nv->c[2] *= 0.25;
nv->c[3] *= 0.25;
nv->n[0] *= 0.25;
nv->n[1] *= 0.25;
nv->n[2] *= 0.25;
dupID = findDuplicateVertex(nv);
if (dupID < 0) {
nv->id = vertexPool.size();
nv->tag = 0;
nv->subLevel = subLevel;
nv->pid = p->pid;
newVertices.push_back(nv->id);
vertexPool.push_back(nv);
} else {
newVertices.push_back(dupID);
}
}
return newVertices;
}
vector<int> CatmullClark::edgeMask(vector<int> vertList,
vector<int> newFacePoints,
vector<int> polyList,
int vertexID,
int subLevel)
{
vector<int> newVertices;
vector<int> faceList;
Vertex *v, *nv, *e, *f0, *f1;
int i, n, id, dupID;
newVertices.clear();
v = vertexPool[vertexID];
n = newFacePoints.size();
for (i=0; i<n; ++i) {
e = vertexPool[vertList[i]];
nv = new Vertex();
f0 = vertexPool[newFacePoints[i]];
id = findAdjacentFaceID(polyList, vertexID, e->id);
f1 = vertexPool[newFacePoints[id]];
if (v->tag == Vertex::Crease &&
e->tag == Vertex::Crease) {
nv->p[0] = (v->p[0] + e->p[0]) * 0.5;
nv->p[1] = (v->p[1] + e->p[1]) * 0.5;
nv->p[2] = (v->p[2] + e->p[2]) * 0.5;
nv->c[0] = (v->c[0] + e->c[0]) * 0.5;
nv->c[1] = (v->c[1] + e->c[1]) * 0.5;
nv->c[2] = (v->c[2] + e->c[2]) * 0.5;
nv->c[3] = (v->c[3] + e->c[3]) * 0.5;
nv->n[0] = (v->n[0] + e->n[0]) * 0.5;
nv->n[1] = (v->n[1] + e->n[1]) * 0.5;
nv->n[2] = (v->n[2] + e->n[2]) * 0.5;
nv->tag = Vertex::Crease;
} else {
nv->p[0] = (v->p[0]+e->p[0]+f0->p[0]+f1->p[0]) * 0.25;
nv->p[1] = (v->p[1]+e->p[1]+f0->p[1]+f1->p[1]) * 0.25;
nv->p[2] = (v->p[2]+e->p[2]+f0->p[2]+f1->p[2]) * 0.25;
nv->c[0] = (v->c[0]+e->c[0]+f0->c[0]+f1->c[0]) * 0.25;
nv->c[1] = (v->c[1]+e->c[1]+f0->c[1]+f1->c[1]) * 0.25;
nv->c[2] = (v->c[2]+e->c[2]+f0->c[2]+f1->c[2]) * 0.25;
nv->c[3] = (v->c[3]+e->c[3]+f0->c[3]+f1->c[3]) * 0.25;
nv->n[0] = (v->n[0]+e->n[0]+f0->n[0]+f1->n[0]) * 0.25;
nv->n[1] = (v->n[1]+e->n[1]+f0->n[1]+f1->n[1]) * 0.25;
nv->n[2] = (v->n[2]+e->n[2]+f0->n[2]+f1->n[2]) * 0.25;
nv->tag = Vertex::Regular;
}
dupID = findDuplicateVertex(nv);
if (dupID < 0) {
nv->id = vertexPool.size();
nv->subLevel = subLevel;
nv->pid = f0->pid;
newVertices.push_back(nv->id);
vertexPool.push_back(nv);
adjacentEdgePoints[f1->id] = nv->id;
} else {
newVertices.push_back(dupID);
adjacentEdgePoints[f1->id] = dupID;
}
}
return newVertices;
}
int CatmullClark::vertexMask(vector<int> vertList,
vector<int> newFacePoints,
int vertexID,
int subLevel)
{
int newVertexID;
Vertex *u, *v, *nv, *nv0, *nv1;
int i, n, k, dupID;
double d;
v = vertexPool[vertexID];
nv = new Vertex();
nv0 = new Vertex();
nv1 = new Vertex();
n = vertList.size();
if (v->tag == Vertex::Crease) {
k = 0;
for (i=0; i<n && k<2; ++i) {
u = vertexPool[vertList[i]];
if (u->tag == Vertex::Crease) {
nv->p[0] += u->p[0] * 0.125;
nv->p[1] += u->p[1] * 0.125;
nv->p[2] += u->p[2] * 0.125;
nv->c[0] += u->c[0] * 0.125;
nv->c[1] += u->c[1] * 0.125;
nv->c[2] += u->c[2] * 0.125;
nv->c[3] += u->c[3] * 0.125;
nv->n[0] += u->n[0] * 0.125;
nv->n[1] += u->n[1] * 0.125;
nv->n[2] += u->n[2] * 0.125;
++k;
}
}
nv->p[0] += v->p[0] * 0.75;
nv->p[1] += v->p[1] * 0.75;
nv->p[2] += v->p[2] * 0.75;
nv->c[0] += v->c[0] * 0.75;
nv->c[1] += v->c[1] * 0.75;
nv->c[2] += v->c[2] * 0.75;
nv->c[3] += v->c[3] * 0.75;
nv->n[0] += v->n[0] * 0.75;
nv->n[1] += v->n[1] * 0.75;
nv->n[2] += v->n[2] * 0.75;
nv->tag = Vertex::Crease;
} else {
// compute (average of vertList) / n
//
for (i=0; i<n; ++i) {
v = vertexPool[vertList[i]];
nv0->p[0] += v->p[0];
nv0->p[1] += v->p[1];
nv0->p[2] += v->p[2];
nv0->c[0] += v->c[0];
nv0->c[1] += v->c[1];
nv0->c[2] += v->c[2];
nv0->c[3] += v->c[3];
nv0->n[0] += v->n[0];
nv0->n[1] += v->n[1];
nv0->n[2] += v->n[2];
}
d = 1.0 / (double)(n*n);
nv0->p[0] *= d;
nv0->p[1] *= d;
nv0->p[2] *= d;
nv0->c[0] *= d;
nv0->c[1] *= d;
nv0->c[2] *= d;
nv0->c[3] *= d;
nv0->n[0] *= d;
nv0->n[1] *= d;
nv0->n[2] *= d;
n = newFacePoints.size();
// compute (average of newFacePoints) / n
//
for (i=0; i<n; ++i) {
v = vertexPool[newFacePoints[i]];
nv1->p[0] += v->p[0];
nv1->p[1] += v->p[1];
nv1->p[2] += v->p[2];
nv1->c[0] += v->c[0];
nv1->c[1] += v->c[1];
nv1->c[2] += v->c[2];
nv1->c[3] += v->c[3];
nv1->n[0] += v->n[0];
nv1->n[1] += v->n[1];
nv1->n[2] += v->n[2];
}
d = 1.0 / (double)(n*n);
nv1->p[0] *= d;
nv1->p[1] *= d;
nv1->p[2] *= d;
nv1->c[0] *= d;
nv1->c[1] *= d;
nv1->c[2] *= d;
nv1->c[3] *= d;
nv1->n[0] *= d;
nv1->n[1] *= d;
nv1->n[2] *= d;
// compute the new vertex
//
v = vertexPool[vertexID];
n = vertList.size();
d = ((double)n - 2.0) / (double)n;
nv->p[0] = nv0->p[0] + nv1->p[0] + v->p[0]*d;
nv->p[1] = nv0->p[1] + nv1->p[1] + v->p[1]*d;
nv->p[2] = nv0->p[2] + nv1->p[2] + v->p[2]*d;
nv->c[0] = nv0->c[0] + nv1->c[0] + v->n[0]*d;
nv->c[1] = nv0->c[1] + nv1->c[1] + v->n[1]*d;
nv->c[2] = nv0->c[2] + nv1->c[2] + v->n[2]*d;
nv->c[3] = nv0->c[3] + nv1->c[3] + v->n[3]*d;
nv->n[0] = nv0->n[0] + nv1->n[0] + v->n[0]*d;
nv->n[1] = nv0->n[1] + nv1->n[1] + v->n[1]*d;
nv->n[2] = nv0->n[2] + nv1->n[2] + v->n[2]*d;
nv->tag = Vertex::Regular;
}
dupID = findDuplicateVertex(nv);
if (dupID < 0) {
nv->id = vertexPool.size();
nv->subLevel = subLevel;
newVertexID = nv->id;
vertexPool.push_back(nv);
} else {
newVertexID = dupID;
}
delete nv0;
delete nv1;
return newVertexID;
}
[21] Farin, G., Curves and Surfaces for Computer-Aided Geometric Design: A
Practical Guide, Fourth Edition, Academic Press, San Diego, 1997
[65] Biermann, Henning, David Zorin, and Adi Levin, Piecewise Smooth
Subdivision Surfaces with Normal Control, ACM Computer Graphics, SIGGRAPH 2000
Proceedings, 34(4):113 - 120
[66] Bolz, Jeffrey and Peter Schöder, Rapid evaluation of Catmull-Clark
subdivision surfaces, 3D technologies for the World Wide Web Proceeding of
the seventh international conference on 3D Web technology, 11 - 17, 2002
[67] Catmull, Ed and James H. Clark, Recursively Generated B-spline Surfaces
on Arbitrary Topological Meshes, Computer Aided Design, 10(6):350- 355,
1978
[68] Chaikin, George M., An algorithm for high speed curve generation, Computer
Vision, Graphics and Image Processing, 3(4):346 - 349, 1974
[69] Clark, James. H., A Fast Algorithm for Rendering Parametric Surfaces,
NASA/Ames Research Centre, 1979
[70] Doo, Donald, A Subdivision Algorithm for Smoothing Down Irregularly Shaped
Polyhedrons, Proceedings on Interactive Techniques in Computer Aided Design,
157-165, 1978
[71] Doo, Donald and Malcolm Sabin, Analysis of the Behavior of Recursive
Division Surfaces Near Extraordinary Points, Computer Aided Design,
10(6):356 - 360, 1978
[72] Gemma, Erich, Richard Helm, Ralph Johnson and John Vlissides,
Design Patterns: elements of reusable object-oriented software,
Boston, MA, Copyright © 1995 by Addison-Wesley
[73] Halstead, Mark, Michael Kass and Tony DeRose, Efficient, Fair
Interpolation Using Catmull-Clark Surfaces, International Conference on
Computer Graphics and Interactive Techniques, Proceedings of the 20th Annual
Conference on Computer Graphics and Interactive Techniques, 35 - 44, 1993
[74] Havemann, Sven, Interactive Rendering of Catmull-Clark Surfaces with
Crease Edges, TUBSCG-2001-11, Institute of Computer Graphics, TU Braunschweig,
Germany, February 2001
[75] Qin, Hong, Chhandomay Mandal and Baba C. Vemuri, Dynamic Catmull-Clark
Subdivision Surfaces, IEEE Transactions on Visualisation and Computer Graphics,
4(3):215 - 229, July - September, 1998
[76] Sederberg, Thomas W., Jianmin Zheng, David Sewell and Malcolm Sabin,
Non-Uniform Recursive Subdivision Surfaces, ACM Computer Graphics, SIGGRAPH
1998 Proceedings, 32(4):387 - 394
[77] Stam, Jos, Exact Evaluation of Catmull-Clark Subdivision Surfaces at
Arbitrary Parameter Values, ACM Computer Graphics, SIGGRAPH 1998 Proceedings,
32(4):395 - 404
[78] Zorin, Denis and Peter Schroder, Subdivision for Modeling and Animation,
SIGGRAPH 2000 Course Notes
2003.03.24
Almost two decades ago, Liang and Barsky developed a fast and efficient parametric line clipping algorithm. The clip region is an upright rectangle [79, 80]. This article is an overview of the algorithm. The region is defined by edges ei having outward pointing normals ni.
Given a line segment clipped against ei the intersection point is
![]()
To solve for t consider the point pEi on edge ei. The dot product
![]()
is equal to zero. Substituting for P(t) we get
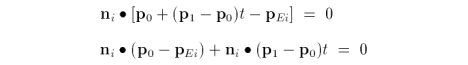
Letting D = p1 - p0 gives rise to
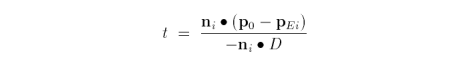
The above equation can be used to find the intersection(s) between the line segment and each edge of the rectangle. In this case, at most, four values of t are generated. The next step is to determine which values of t correspond to an intersection with the clip rectangle. We can classify these points as either potentially entering (PE) or potentially leaving (PL) such that
- if moving from p0 to p1 causes us to enter the clip edge, the point is PE.
- if moving from p0 to p1 causes us to leave the clip edge, the point is PL.
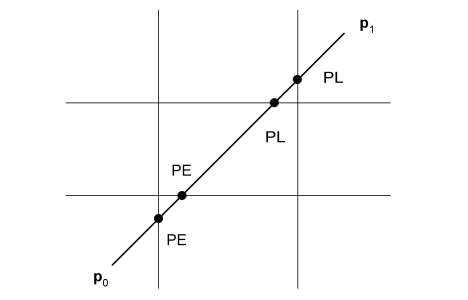
- a point is PE if the dot product ni . D is less than zero.
- a point is PL if the dot product ni . D is greater than zero
The line we want is defined by a (PE, PL) pair where the following conditions are true:
t E = 0 is the lower bound of PE
t L = 1 is the upper bound of PL
t E is less than t L
These conditions describe the algorithm's trivial rejection criteria. The algorithm can be extended to clip a line in three dimensional space against the six clipping planes of a view frustum.
As paraphrased from the GNU General Public License "the following instances of program code are distributed in the hope that it will be useful, but without any warranty; without even the implied warranty of merchantability or fitness for a particular purpose." Please do not hesitate to notify me of any errors in logic and/or semantics.
// ----------------------------------------------------------
// liangBarsky.h (two dimensional only)
// ----------------------------------------------------------
#ifndef __LIANG_BARSKY__H__
#define __LIANG_BARSKY__H__
typedef struct {
double x, y, z;
} Point;
class LiangBarsky
{
public:
LiangBarsky();
LiangBarsky(double, double);
~LiangBarsky();
void clipLine(Point *, Point *);
private:
double xmin, xmax, ymin, ymax;
int isZero(double);
int pointInside(Point *);
int clipT(double, double, double *, double *);
};
inline int LiangBarsky::isZero(double a)
{
return ( (a) < 0.000001 && (a) > -0.000001 );
}
inline int LiangBarsky::pointInside(Point *a)
{
return (a->x >= xmin && a->x <= xmax &&
a->y >= ymin && a->y <= ymax);
}
#endif // __LIANG_BARSKY__H__
// ----------------------------------------------------------
// liangBarsky.cpp (two dimensional only)
// ----------------------------------------------------------
#include "liangBarsky.h"
LiangBarsky::LiangBarsky()
{
xmin = 0.0;
xmax = 800.0;
ymin = 0.0;
ymax = 600.0;
}
LiangBarsky::LiangBarsky(double x, double y)
{
xmin = 0.0;
xmax = (x <= 0.0) ? 800.0 : x;
ymin = 0.0;
ymax = (y <= 0.0) ? 600.0 : y;
}
LiangBarsky::~LiangBarsky() { }
void LiangBarsky::clipLine(Point *a, Point *b)
{
double dx, dy, tE, tL;
dx = b->x - a->x;
dy = b->y - a->y;
if (isZero(dx) && isZero(dy) && pointInside(a)) return;
tE = 0;
tL = 1;
if (clipT(xmin - a->x, dx, &tE, &tL) &&
clipT(a->x - xmax, -dx, &tE, &tL) &&
clipT(ymin - a->y, dy, &tE, &tL) &&
clipT(a->y - ymax, -dy, &tE, &tL))
{
if (tL < 1) {
b->x = a->x + tL * dx;
b->y = a->y + tL * dy;
}
if (tE > 0) {
a->x += tE * dx;
a->y += tE * dy;
}
}
}
int LiangBarsky::clipT(double num, double denom,
double *tE, double *tL)
{
double t;
if (isZero(denom)) return (num <= 0.0);
t = num / denom;
if (denom > 0) {
if (t > *tL) return 0;
if (t > *tE) *tE = t;
} else {
if (t < *tE) return 0;
if (t < *tL) *tL = t;
}
return 1;
}
[79] Liang, Y.D., and Barsky, B., A New Concept and Method for Line
Clipping," ACM Transactions on Graphics, 3(1):1-22, January 1984
[80] Liang, Y.D., B.A., Barsky, and M. Slater, Some Improvements
to a Parametric Line Clipping Algorithm, CSD-92-688, Computer Science
Division, University of California, Berkeley, 1992