2003.10.07
Motion picture films have become increasing subject to digital manipulation. Old films, for example, are restored to their original luster when artists remove blemishes and other visual artifacts. Colours may be changed and even new objects or characters are added to scenes. Computer image file formats must be able to represent even the most subtle shifts in hue and saturation. To this end, there are specialised file formats that represent colour information at extraordinarily high levels of precision.
Eastman Kodak developed the Cineon film format, a subset of the ANSI/SMPTE 268M-1994 Digital Moving-Picture Exchange (DPX) file format [104, 106]. The headers of a DPX file are generic so that a Cineon file can be easily derived. The file structure of a DPX image consists of four parts:
- generic header: a fixed, predefined, general information header
- SMPTE header: a fixed format header that is specific to the motion picture
and television industry
- user-defined information: variable length, user defined data
- image data
The DPX specification supports five header types. A DPX file, however, does not necessarily contain all five types. Below is a summary of these header structs presented in C/C++ data structure format.
typedef unsigned float R32; // assuming 32-bit precision
typedef unsigned long U32; // assuming 32-bit precision
typedef unsigned short U16; // assuming 16-bit precision
typedef unsigned char U8; // assuming 8-bit precision
// Generic header contains information that can be used by any
// image manipulation program
//
typedef struct generic_header
{
U32 magic_num; // magic number 0x53445058 (SDPX) or
// 0x58504453 (XPDS)
U32 offset; // offset to image data in bytes
char vers[8]; // which header format version is
// being used (v1.0)
U32 file_size; // file size in bytes
U32 ditto_key; // read time short cut - 0 = same,
// 1 = new
U32 gen_hdr_size; // generic header length in bytes
U32 ind_hdr_size; // industry header length in bytes
U32 user_data_size; // user-defined data length in bytes
char file_name[100]; // name of the image file
char create_time[24]; // date of file creation
// (yyyy:mm:dd:hh:mm:ss)
char creator[100]; // name of the creator
char project[200]; // name of the project
char copyright[200]; // copyright string
U32 key; // encryption flag
// (FFFFFFFF = unencrypted)
char Reserved[104]; //
} GenericHeader;
// Image information header describes the number of channels,
// resolution, et cetera of the image
//
typedef struct image_information
{
U16 orientation; // orientation of the image
U16 element_number; // number of image element
U32 pixels_per_line; // or x value
U32 lines_per_image_ele; // or y value, per element
struct image_element
{
U32 data_sign; // data sign
// (0 = unsigned, 1 = signed )
// "Core set images are unsigned"
U32 ref_low_data; // reference low data code value
R32 ref_low_quantity; // reference low quantity
// represented
U32 ref_high_data; // reference high data code value
R32 ref_high_quantity;// reference high quantity
// represented
U8 descriptor; // descriptor for image element
U8 transfer; // transfer characteristics for
// element
U8 colourimetric; // colourmetric specification for
// element
U8 bit_size; // bit size for element
U16 packing; // packing for element
U16 encoding; // encoding for element
U32 data_offset; // offset to data of element
U32 eol_padding; // end of line padding used in
// element
U32 eo_image_padding; // end of image padding used in
// element
char description[32]; // description of element
} image_element[8];
U8 reserved[52];
} ImageInformationHeader;
// Image orientation header indicates how the image data is
// arranged.
//
typedef struct image_orientation
{
U32 x_offset; // X offset
U32 y_offset; // Y offset
R32 x_center; // X center
R32 y_center; // Y center
U32 x_orig_size; // X original size
U32 y_orig_size; // Y original size
char file_name[100]; // source image file name
char creation_time[24]; // source image creation date
// and time
char input_dev[32]; // input device name
char input_serial[32]; // input device serial number
U16 border[4]; // border validity
// (XL, XR, YT, YB)
U32 pixel_aspect[2]; // pixel aspect ratio
// (horizontal:vertical)
U8 reserved[28];
} OrientationHeader;
// There are two Industy headers; one for film/motion picture and
// the other for television broadcasts. These structs define the
// content of the SMPTE-specific portion the DPX file.
//
typedef struct motion_picture_film_header
{
char film_mfg_id[2]; // film manufacturer ID code
// (2 digits from film edge code)
char film_type[2]; // file type
// (2 digits from film edge code)
char offset[2]; // offset in perfs
// (2 digits from film edge code)
char prefix[6]; // prefix
// (6 digits from film edge code)
char count[4]; // count
// (4 digits from film edge code)
char format[32]; // format (i.e. academy)
U32 frame_position; // frame position in sequence
U32 sequence_len; // sequence length in frames
U32 held_count; // held count (1 = default)
R32 frame_rate; // frame rate of original in
// frames per second
R32 shutter_angle; // shutter angle of camera
// in degrees
char frame_id[32]; // frame identification
// (i.e. keyframe)
char slate_info[100]; // slate information
U8 reserved[56];
} FilmIndustryHeader;
typedef struct television_header
{
U32 tim_code; // SMPTE time code
U32 userBits; // SMPTE user bits
U8 interlace; // interlace
// 0 = noninterlaced,
// 1 = 2:1 interlace
U8 field_num; // field number
U8 video_signal; // video signal standard
U8 unused; // used for byte alignment only
R32 hor_sample_rate; // horizontal sampling rate in Hz
R32 ver_sample_rate; // vertical sampling rate in Hz
R32 frame_rate; // temporal sampling rate or frame
// rate in Hz
R32 time_offset; // time offset from sync to
// first pixel
R32 gamma; // gamma value
R32 black_level; // black level code value
R32 black_gain; // black gain
R32 break_point; // breakpoint
R32 white_level; // reference white level code value
R32 integration_times; // integration time(s)
U8 reserved[76];
} TelevisionIndustryHeader;
The user-defined part of a DPX file is rather straight-forward.
typedef struct user_defined_data
{
char UserId[32]; // user-defined identification string
U8 *Data; // user-defined data. the DPX standard
// permits this field may be up to one
// megabyte (MB) in length
} UserDefinedData;
The image data is stored as an array of elements aligned in 32-bit boundaries. Each element may consist of up to four signed or unsigned numeric values. These values represent the component(s) of a given pixel. Valid component sizes are 1-, 8-, 10-, 12-, and 16-bit integers, and 32- and 64-bit IEEE floating point numbers.
A true industry juggernaut and pioneer in digital special effects for motion picture film is Industrial Light & Magic (ILM). The company has proven, over the years, to be innovators in the visual realm of post-production film work. To support their goals, ILM have introduced dozens of key technologies and methods. One such endeavour is OpenEXR, an open-source alternative to DPX and Cineon. There are several attractive features of OpenEXR, some of which are listed below [105]:
high dynamic range: each component of given pixel is stored as a
16- or 32-bit IEEE floating point number. this is significantly more
precise than the typical 8-bit per channel representation in RGBA-centric
file formats.
good colour resolution: with 16-bit floating point numbers, there are
1024 colour resolution steps per f-stop (an f-stop being the adjustment
which changes the diameter of the lens that controls the amount of
light entering the camera). typical 8-bit formats can only represent
less than 70 steps per f-stop
lossless data compression: no information is lost regardless of the
number of file compressions/decompressions.
arbitrary image channels: there is no limit to the number of channels
used to present a given pixel. OpenEXR can, for example, store the
red, green, blue, alpha, luminance, chroma, depth, surface normal
directions and motion vectors on a per-pixel basis.
portability: OpenEXR is hardware and operating system independent.
[104] Cinesite Hollywood (http://www.cinesite.com/).
Kodak, Eastman and Cineon are trademarks of Eastman Kodak Company. Cinesite Ltd.,
is a Kodak Company.
[105] OpenEXR (http://www.openexr.com/). Lucas
Digital Ltd. LLC. OpenEXR, Industrial Light & Magic and ILM are trademarks and
service marks of Lucasfilm Ltd.
[106] SMPTE.org (http://www.smpte.org). Society of
Motion Picture and Television Engineers.
2003.12.12
Methods to illuminate an outdoor scene during the daytime hours is well documented [29, 30, 33, 34, 35, 36, 37]. Less attention has been devoted to accurately depict nighttime outdoor environments. We will briefly touch upon some detail of a simple nightsky model and the associated sources of natural illumination.
People often describe the lighting of a scene with subjective terms. A room can be sombre with its muted colours. A forest glade can be dreamlike in the way shafts of sunlight are filtered through the leaves. A warm and festive mood can be conveyed through the soft glow of a Christmas tree adorned with coloured lights. An outdoor winter scene is said to be crisp if sparkling white snow lies beneath the canopy of a cloudless sky. From these scenarios, it's apparent that light contributes greatly to the mood and feel of an environment. A natural light source with a high colour tempeature conveys a sense of coolness; the Moon for instance. Biochemical light sources usually cast a soft, low temperature colour so they, too, offer a mellow ambiance.
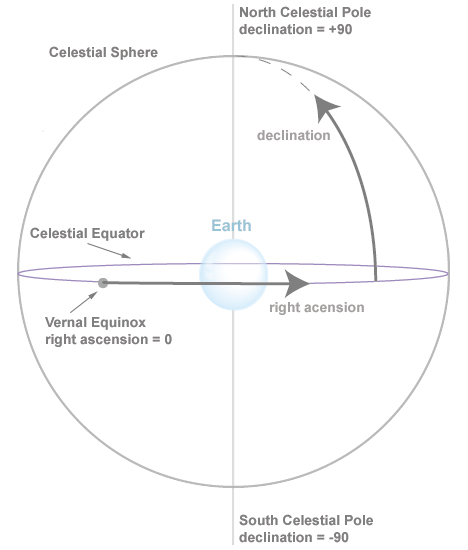
The brightest source of natural light in the nightsky is the Moon. Its orbit is the result of gravitational influences from not only the Earth and the Sun, but also the distant planets of Venus and Jupiter. This interplay of forces require a highly complex set of formulae to model the Moon's orbit. The location of the Moon, as seen from Earth, is described by a pair of coordinates: right ascension and declination. Definitions of these and related terms are provided in section 14.4 Glossary. The illustration below details for the relationship between right ascension and declination. Right ascension is measured eastward from the vernal equinox. Declination is measured from the celestial equator.
The Moon is not a direct source of light; rather, it reflects and scatters sunlight. The Hapke-Lommel-Seeliger bidirectional reflectance distribution function (BRDF) is used to model the light scattering [31, 45]. Assuming the angle between surface normal n and incident light is θi and the angle between n and reflected light is θr, the BRDF is
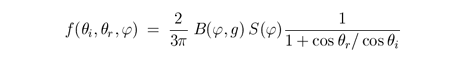
where φ is angle between ωi and ωo. B(φ, g) is called the retrodirective function
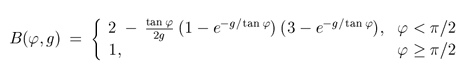
g is the surface density parameter that controls the intensity of reflected light. The valid range for this parameter is [0.4, 0.8] with 0.6 being ideal [31]. S(φ) is the scattering law
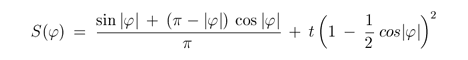
where t controls the amount of forward scattering of light and should be set to 0.1 [31].
Using the Lommel-Seeliger law to compute the irradiance [W / m2] from the Moon at phase angle φ and distance d, we use the following equation
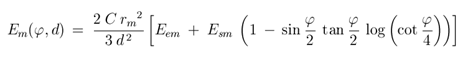
where rm is the radius of the Moon, and C is its average albedo (C = 0.072).
Esm is the irradiance of the Sun on the surface of the Moon, and Eem is earthshine
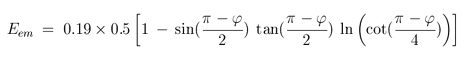
where φ is angle between ωi and ωo. Some typical values of irradiance are
| Component | Irradiance [W / m2] |
| Sunlight * | 1.4 x 10 3 |
| Sunlight ** | 1.0 x 10 3 |
| Full Moon | 2.1 x 10 -3 |
| Bright planets | 2.0 x 10 -6 |
| Integrated starlight | 3.0 x 10 -8 |
| * The atmosphere of the Moon is very light, so the Moon receives much of its irradiance from the Sun unfiltered. Precise measurements have been made, with published values in the range of 1370 to 1410 watts per square meter. | |
| ** The atmosphere of the Earth filters about 25% of the light energy from the Sun, including most solar ultraviolet (UV) radiation. As such, the Earth receives about 1000 watts of power per square meter. Due to ozone layer depletion the North and South Poles receive more irradiance. | |
As observed from the surface of Earth, the Moon resembles an area light source with exponential dropoff. The colour of moonlight is the colour of the sunlight but with much less intensity. A scene illuminated by moonlight appears desaturated. Colours are muted and exhibit a blue-shift. An algorithm that performs this shift should operate in CIE XYZV colour space. An alternative is to perform the shift in RGBA space as shown in the following pseudocode.
applyBlueShift()
{
for each RGBA element {
c[0] = red
c[1] = green
c[2] = blue
// stage one
//
s[] = c[] in ascending order where s[0] is the minimum
d[0] = (c[0] - s[0]) / 2
d[1] = (c[1] - s[0]) / 2
d[2] = (c[2] - s[0]) / 2
c[0] = s[0] + d[0]
c[1] = s[0] + d[1]
c[2] = s[0] + d[2]
// stage two
//
s[] = c[] in decending order where s[0] is the maximum
d[0] = (c[0] - s[0]) / 2
d[1] = (c[1] - s[0]) / 2
d[2] = (c[2] - s[0]) / 2
c[0] = s[0] + d[0]
c[1] = s[0] + d[1]
c[2] = s[0] + d[2]
// update the RGBA element; no change to alpha
//
red = c[0]
green = c[1]
blue = c[2]
}
}
Here are some colour swatches to illustrate the result of applying the blue-shift process within RGBA space. The left swatch is the original colour (in sunlight) and the middle swatch is the colour after stage one. In moonlight only, the colour appears as it does in the right swatch. Notice the desaturation.



Some organisms are bioluminescent, an ability where they can actively or passively trigger a set of chemical reactions to emit light. Fireflies use their bioluminescence during their courtship rituals. Females flash about every two seconds; males flash about every five seconds. These insects have an organ called the abdominal lantern [108]. Light production involves a rather complex luciferin-luciferase reaction between adenosine triphosphate (ATP) and oxygen occuring within the photocytes of the abdominal lantern [112]. The colour of firefly light is a bright yellow-green and is often modeled as a point light source. The illuminance of firefly light is 0.025 of a candela; its irradiance is only 3.7E-5 watts per square meter per steradian.
Certain species of fungi are bioluminescent. They require high humidity climates with almost complete shade cover to survive. The luciferin-luciferase reaction within these fungi yields a pale blue-green light, modeled as an area light source. The illuminance and irradiance of fungi light is slightly less than that of firefly light.
As paraphrased from the GNU General Public License "the following instances of program code are distributed in the hope that it will be useful, but without any warranty; without even the implied warranty of merchantability or fitness for a particular purpose." Please do not hesitate to notify me of any errors in logic and/or semantics.
The most direct use of the code herein is to instantiate a Moon object and then invoke computeMoonPosition() as follows:
#include "Observer.h"
#include "Moon.h"
int main(int argc, char *argv[])
{
// latitude: 43.67 degrees
// longitude: -79.39 degrees
// date: December 25, 2003
// time: 00:30:00 UT
Observer *o = new Observer(43.67, -79.39, 2003, 12, 25,
0, 30, 0);
Moon *m = new Moon();
m->computeMoonPosition(o);
delete o;
delete m;
return 0;
}
All source files are available for download.
// ----------------------------------------------------------
// Observer.h
// ----------------------------------------------------------
#pragma once
#ifndef __OBSERVER_H__
#define __OBSERVER_H__
class Observer
{
public:
Observer(double, double, int, int, int, int, int, int);
~Observer(void);
double getLatitude();
double getLongtitude();
int getYear();
int getMonth();
int getDay();
int getHour();
int getMinute();
int getSecond();
private:
double latitude;
double longitude;
int year;
int month;
int day;
int hour;
int minute;
int second;
};
inline double Observer::getLatitude() { return latitude; }
inline double Observer::getLongtitude() { return longitude; }
inline int Observer::getYear() { return year; }
inline int Observer::getMonth() { return month; }
inline int Observer::getDay() { return day; }
inline int Observer::getHour() { return hour; }
inline int Observer::getMinute() { return minute; }
inline int Observer::getSecond() { return second; }
#endif // __OBSERVER_H__
// ----------------------------------------------------------
// Observer.cpp
// ----------------------------------------------------------
//#include "stdafx.h"
#include "Observer.h"
Observer::Observer(double lat, double lon,
int yr, int mth,
int dy, int hr,
int min, int sec)
{
latitude = lat;
longitude = lon;
year = yr;
month = mth;
day = dy;
hour = hr;
minute = min;
second = sec;
}
Observer::~Observer(void) { }
// ----------------------------------------------------------
// Moon.h
// ----------------------------------------------------------
#pragma once
#ifndef __MOON_H__
#define __MOON_H__
#include "Observer.h"
#define _USE_MATH_DEFINES // required by Visual Studio .NET
#include <math.h> // to access math.h constant M_PI
//
// those using gcc should use the
// -lm option during compilation
class Moon
{
public:
Moon(void);
~Moon(void);
void computeMoonPosition(Observer *);
double getRightAscension();
double getDeclination();
private:
double getDays(int, int, int, double);
double getAngle(double, double);
double getRange(double);
int getInteger(double);
// the right ascension of the Moon is the angular
// distance eastward along the celestial equator from
// the vernal equinox to the intersection of the hour
// circle that passes through the body; expressed in
// hours and minutes and seconds (hh.mmss)
//
// the declination of the Moon is the angular distance
// to a point on a celestial object measured north or
// south from the celestial equator; expressed in
// degrees (ddd.mmss); used with right ascension to
// specify positions on the celestial sphere
//
// EXAMPLE:
//
// latitude: 43.67 degrees
// longitude: -79.39 degrees
// date: December 12, 2003
// time: 00:30:00 UT
//
// topocentric right ascension = 7.85358
// = 7 hours, 51 minutes,
// 12.8872 seconds
//
// topocentric declination = 25.2242
// = 25 degrees, 13 minutes,
// 27.1306 seconds
//
double rightAscensionGEO; // geocentric
double declinationGEO; //
double rightAscensionTOPO; // topocentric
double declinationTOPO; //
};
inline double Moon::getRightAscension()
{
return rightAscensionTOPO;
}
inline double Moon::getDeclination()
{
return declinationTOPO;
}
// get the number of days to December 31 0h 2000
// h is UT in decimal hours
// valid for the 20th and 21st centuries
inline double Moon::getDays(int y, int m, int d, double h)
{
long val = - 7 * (y + (m + 9) / 12) / 4 + 275 * m / 9 + d;
val += y * 367;
return (double)(val - 730530.0 + h / 24.0);
}
// return the angle in the range [0, 2M_PI] depending on
// the signs of x and y
inline double Moon::getAngle(double y, double x)
{
double a;
a = atan(y / x);
if (x < 0.0) a += M_PI;
if (y < 0.0 & & x > 0.0) a += (2*M_PI);
return a;
}
// return an angle in the range [0, 2M_PI]
inline double Moon::getRange(double x)
{
double b;
double a;
double tpi;
tpi = 2 * M_PI;
b = x / tpi;
a = tpi * (b - getInteger(b));
if (a < 0.0) a += tpi;
return a;
}
// return the integer part of a double
inline int Moon::getInteger(double x)
{
int sign;
int val;
sign = (x < 0.0) ? -1 : 1;
val = (int)abs(x);
return sign * val;
}
#endif // __MOON_H__
// ----------------------------------------------------------
// Moon.cpp
//
// based on prior work by Keith Burnett and Paul Schlyter
// (c) 1998
// ----------------------------------------------------------
//#include "stdafx.h"
#include "Moon.h"
Moon::Moon(void) { }
Moon::~Moon(void) { }
void Moon::computeMoonPosition(Observer *o)
{
double degs = 180.0 / M_PI;
double rads = M_PI / 180.0;
// get time and date
double h = o->getHour();
h = h + o->getMinute() / 60.0;
double d = getDays(o->getYear(), o->getMonth(),
o->getDay(), h);
// Moon elements
// longitude of the Moon's node
double Nm = getRange((125.1228 - 0.0529538083 * d) *
rads);
double im = 5.1454 * rads;
// argument for the perihelion of the Moon
double wm = getRange((318.0634 + 0.1643573223 * d) *
rads);
// Earth radii
double am = 60.2666;
double ecm = 0.0549;
// mean anomoly of the Moon
double Mm = getRange((115.3654 + 13.0649929509 * d) *
rads);
// Sun elements
double Ns = 0.0;
double isun = 0.0;
// argument for the perihelion of the Sun
double ws = getRange((282.9404 + 0.0000470935 * d) *
rads);
// one Astronomical Unit
double asun = 1.0;
double ecs = 0.016709 - 0.000000001151 * d;
// mean anomoly of the Sun
double Ms = getRange((356.047 + 0.9856002585 * d) *
rads);
// position of the Moon
double Em = Mm + ecm * sin(Mm) * (1.0 + ecm * cos(Mm));
double xv = am * (cos(Em) - ecm);
double yv = am * (sqrt(1.0 - ecm * ecm) * sin(Em));
double vm = getAngle(yv, xv);
double rm = sqrt(xv * xv + yv * yv);
double xh = rm * (cos(Nm) * cos(vm + wm) - sin(Nm) *
sin(vm + wm) * cos(im));
double yh = rm * (sin(Nm) * cos(vm + wm) + cos(Nm) *
sin(vm + wm) * cos(im));
double zh = rm * (sin(vm + wm) * sin(im));
// the geocentric longitude and latitutde of the Moon
double lon = getAngle(yh, xh);
double lat = getAngle(zh, sqrt(xh * xh + yh * yh));
// perturbations in radians
// mean longitude of the Sun
double Ls = Ms + ws;
// mean longitude of the Moon
double Lm = Mm + wm + Nm;
// mean elongation of the Moon
double dm = Lm - Ls;
// argument of the latitude for the Moon
double F = Lm - Nm;
// add the following terms to the longitude
// note amplitudes are in degrees, convert at end
double dlon;
// evection
dlon = -1.274 * sin(Mm - 2.0 * dm);
// variation
dlon = dlon + 0.658 * sin(2.0 * dm);
// yearly equation
dlon = dlon - 0.186 * sin(Ms);
dlon = dlon - 0.059 * sin(2.0 * Mm - 2.0 * dm);
dlon = dlon - 0.057 * sin(Mm - 2.0 * dm + Ms);
dlon = dlon + 0.053 * sin(Mm + 2.0 * dm);
dlon = dlon + 0.046 * sin(2.0 * dm - Ms);
dlon = dlon + 0.041 * sin(Mm - Ms);
// parallactic equation
dlon = dlon - 0.035 * sin(dm);
dlon = dlon - 0.031 * sin(Mm + Ms);
dlon = dlon - 0.015 * sin(2.0 * F - 2.0 * dm);
dlon = dlon + 0.011 * sin(Mm - 4.0 * dm);
lon = dlon * rads + lon;
// latitude terms
double dlat;
dlat = -0.173 * sin(F - 2 * dm);
dlat = dlat - 0.055 * sin(Mm - F - 2.0 * dm);
dlat = dlat - 0.046 * sin(Mm + F - 2.0 * dm);
dlat = dlat + 0.033 * sin(F + 2.0 * dm);
dlat = dlat + 0.017 * sin(2.0 * Mm + F);
lat = dlat * rads + lat;
// distance terms Earth radii
rm = rm - 0.58 * cos(Mm - 2.0 * dm);
rm = rm - 0.46 * cos(2.0 * dm);
// find the cartesian coordinates
// of the geocentric lunar position
double xg = rm * cos(lon) * cos(lat);
double yg = rm * sin(lon) * cos(lat);
double zg = rm * sin(lat);
// rotate to equatorial coords
// obliquity of ecliptic of date
double ecl = (23.4393 - 0.0000003563 * d) * rads;
double xe = xg;
double ye = yg * cos(ecl) - zg * sin(ecl);
double ze = yg * sin(ecl) + zg * cos(ecl);
// geocentric right ascension and declination
double ra = getAngle(ye, xe);
double dec = atan(ze / sqrt(xe * xe + ye * ye));
rightAscensionGEO = ra * degs / 15.0;
declinationGEO = dec * degs;
// topocentric right ascension and declination
double lst = 100.46 + 0.985647352 * d + h * 15.0 +
o->getLongtitude();
lst = getRange(lst * rads);
double glat = o->getLatitude() * rads;
double glong = o->getLongtitude() * rads;
double xtop = xe - cos(glat) * cos(lst);
double ytop = ye - cos(glat) * sin(lst);
double ztop = ze - sin(glat);
double ratop = getAngle(ytop, xtop);
double dectop = atan(ztop / sqrt(xtop * xtop +
ytop * ytop));
rightAscensionTOPO = ratop * degs / 15.0;
declinationTOPO = dectop * degs;
}
[29] Bryan, Harvey and Sayyed Mohammed Autif, Lighting/Daylighting Analysis:
A Comparison, School of Architecture, Arizona State University, 2002
[30] Daubert, Katja, Hartmut Schirmacher, François X. Sillion, and George
Drettakis, Hierarchical Lighting Simulation for Outdoor Scenes, 8th
Eurographics workshop on Rendering, 1997
[31] Jensen, Henrik Wann, Frédo Durand, Michael M. Stark, Simon
Premože, Julie Dorsey and Peter Shirley, A Physically-Based Night Sky
Model, ACM Computer Graphics, SIGGRAPH 2001 Proceedings, 35(4):399-408
[33] Kaneda, Kazufumi, Takashi Okamoto, Eihachiro Nakamae and Tomoyuki
Nishita, Highly Realistic Visual Simulation of Outdoor Scenes Under
Various Atompsheric Conditions, Proceedings of the eighth international
conference of the Computer Graphics Society on CG International '90:
computer graphics around the world, 117-131, 1990
[34] Nishita, Tomoyuki, Yoshinori Dobashi, Kazufumi Kaneda and Hideo
Yamashita, Display Method of the Sky Color Taking into Account
Multiple Scattering, Faculty of Engineering, Fukuyama University, Japan,
December 27, 2000
[35] Nishita, Tomoyuki, Eihachiro Nakamae, Continuous Tone Representation
of Three-Dimensional Objects Illuminated by Sky Light, ACM Computer
Graphics, SIGGRAPH 1986 Proceedings, 20(4):125-131
[36] Preetham, A.J., Peter Shirley and Brian Smits, A Practical Analytic
Model for Daylight, Department of Computer Science, University of Utah,
1999
[37] Tadamura, Katsumi, Eihachiro Nakamae, Kazufumi Kaneda, Masashi
Babam Hideo Yamashita and Tomoyuki Nishita, Modeling of Skylight and
Rendering of Outdoor Scenes, Eurographics 1993, 12(3):189-200
[45] Hashemi, Leila, Ali Aziz and Mohammad Hasan Hashemi, Implementation of a
Single Photo Shape from Shading Method for the Automatic DTM Generation, PCV02
Photogrammetric Computer Vision, ISPRS Commission III, Symposium 2002
[107] Ashikhmin, Michael, A Tone Mapping Algorithm for High Contrast
Images, 11th Eurographics Workshop on Rendering, 2002, 1 - 11
[108] Buck, J. H., Annals of the New York Academy of Sciences 49:397, 1949
[109] Debevec, Paul E., Rendering Synthetic Objects into Real Scenes:
Bridging Traditional and Image-Based Graphics with Global Illumination
and High Dynamic Range Photography. ACM Computer Graphics, SIGGRAPH 1998
Proceedings, 32(4):189 - 198
[110] Jang, Hin - 4 Outdoor Lighting (ttps://hinjang.com/articles/02.html#four)
[111] Nguyen, Duc, Doug Enright and Ron Fedkiw, Simulation and Animation
of Fire and Other Natural Phenomena in the Visual Effects Industry,
Western States Section, Combustion Institute, Fall Meeting, UCLA, 2003
[112] Wilson, T., and J.W. Hastings, Annual Review of Cell and Developmental Biology,
381:745, 1998
albedo The fraction of incident light energy reflected off a surface. The average albedo of the Moon, for example, is 0.072 or 7.2 percent.
celestial equator The projection of the Earth's equator onto the sky. The declination coordinate is an angle measured with respect to the celestial equator.
celestial pole The celestial poles are the projections of the Earth's north and south poles into the celestial sphere.
celestial sphere The projection of objects in space into their apparent positions in the sky as viewed from the Earth.
constellation of Pisces The grouping of stars, resembling a pair of fish, located near 1hr right ascension and 15° declination.
declination The angular distance to a point on a celestial object measured north or south from the celestial equator; expressed in degrees; used with right ascension to specify positions on the celestial sphere. Declination is measured from -90° (projected south pole) to +90° (projected north pole).
ecliptic The region of the sky corresponding to the projection of the ecliptic plane.
ecliptic plane The plane of the Earth's orbit around the Sun. The portion of the sky lying in the ecliptic plane is called the zodiac (or sometimes the ecliptic). The orbits of the other planets (except for Pluto) are also in the ecliptic plane, so their paths on the sky all lie in this plane. The collection of constellations lying along the ecliptic plane is called the zodiac.
hour angle The angle between an observer's meridian and the hour circle on which some celestial body lies. This angle is conventionally expressed in units of time (hours, minutes, and seconds), which gives the time elapsed since the celestial body's last transit at the observer's meridian (for a positive hour angle), or the time unit the next transit (for a negative hour angle).
hour circle A great circle passing through the celestial poles. The position of the hour circle and the azimuthal coordinate of a celestial body lying on it is specified by its right ascension.
great circle A section of a sphere that contains a diameter of the sphere.
meridian A great circle passing over the zenith and through the celestial poles.
prime meridian The zero point for longitude on the Earth, defined as the longitude of the Greenwich Royal Observatory in England.
right ascension The angular distance eastward along the celestial equator from the vernal equinox to the intersection of the hour circle that passes through the body. The azimuthal angle at which the hour circle of a celestial object is located. The rotation axis taken as the direction of the celestial pole. Right ascension is usually measured in units of time (hours, minutes, and seconds), with one hour of time approximately equal to 15° of arc. The zero point of right ascension is the arbitrary direction in the reference plane at which right ascension is defined as 0. During the early 21st century, the zero point of right ascension is near the constellation of Pisces.
rising knot The closed, non-self-intersecting path of a celestial object, as seen from the Earth, that cannot be untangled to produce a simple loop.
vernal equinox The point on the celestial sphere where the center of the Sun crosses the celestial equator moving southward as seen from the southern hemisphere. The point on the celestial sphere where the paths of the ecliptic and the celestial equator cross near the constellation of Pisces.
zodiac The portion of the sky which lies along the Earth's ecliptic plane.
