2005.08.08
Display devices have a limited gamut of intensities. Our eyes, however, are much more sensitive by several orders of magnitude. To better mimic how we perceive colour in the real-world we use high dynamic range (HDR) rendering. The dynamic range is the ratio between the maximum and minimum intensities. We can increase the overall perceived contrast of a scene by making local changes to contrast. There are several ways to approach HDR rendering, two of which are described herein.
The amount of light we see is controlled by the round and contractile membrane of the eye commonly known as the iris. Under well illuminated conditions the iris contracts, otherwise it dilates. Also important in how we perceive the world is the amount of time we view a scene. We notice, for example, that features in a dark room become more evident the longer we look around. In our model we use exposure T to represent the contraction / dilation of our irises and the amount of time we view a particular scene. We render very intense sources of light with large values of T. To underexpose parts of a scene we use small values of T. The relationship between intensity and the amount of light can be simplified to
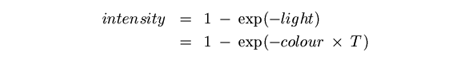
This equation describes a tone reproduction curve [114]. For each colour channel of a given pixel we apply the following spatially invariant transform
double expose(double colour, double T)
{
if (colour < 0.0 || T < 0.0) return 0.0;
return (1.0 - exp(-colour * T)) * 255.0; // assuming 8-bit precision
}
Graphics APIs such as OpenGL 2.0 and DirectX 9.0c consist of a fragment programming model where per-pixel operations like those illustrated in expose() can be done in hardware.
HDR lighting effects can also be achieved using floating point textures. These render targets support values outside the 0.0 to 1.0 range. The algorithm is rather straightforward and can be fully realised within a fragment program.
- Downsample the original scene (OS) by averaging each 4 x 4 block of texels. Store the result in a floating point (FP) texture. Use larger texel blocks to reduce the amount of calculations.
- Compute the average luminance of FP
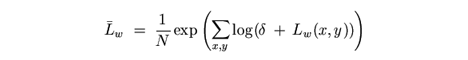
where N is the total number of texels in FP. The coordinates of a given texel are (x, y) and δ is a small value to avoid the singularity that occurs when Lw(x,y) = 0.
- Tone map FP to create floating point texture FP2. The tone map operator is
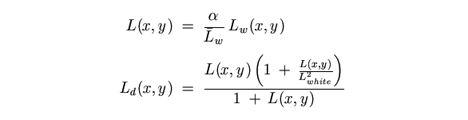
where L(x, y) is a scaled luminance in FP. Lwhite is the smallest luminance in FP that is mapped to white. Typical values of α are within the 0.18 to 0.72 range [115].
- Downsample FP2 by averaging each 2 x 2 block of texels. Apply a Guassian blur along the horizontal and then the vertical. Upsample FP2 back to the size of OS using bilinear filtering.
- Combine FP2 and OS for final display.
The OpenEXR file format supports 16- and 32-bits per channel to yield several quadrillion possible colour permutations. Real-world luminance information can thus be stored. An image gallery of HDR renders is available at Render-Art.
[113] Debevec, P., and J. Malik. Recovering High Dynamic Range Radiance Maps
from Photographs, ACM Computer Graphics, SIGGRAPH 1997 Proceedings,
31(4):369-378
[114] DiCarlo, J.M., and B.A. Wandell, Rendering High Dynamic Range Images,
Proceedings of the SPIE: Image Sensors, 3965:189-198
[115] Reinhard, E., M. Stark, P. Shirley, and J. Ferwerda, Photographic Tone
Reproduction for Digital Images, ACM Transactions on Graphics,
21(3):267-276
2002.12.07
The surface is defined by the function
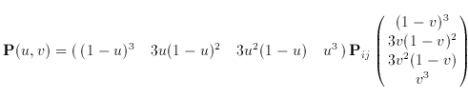
where u and v vary in the range from zero to one. The control net is
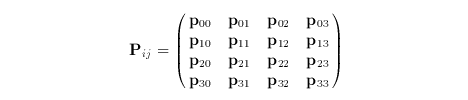
An alternate form is
![]()
where
![]()
and
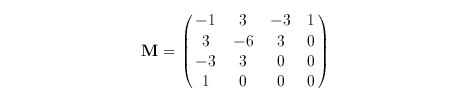
2002.12.07
The surface is defined by the function

where u and v vary in the range from zero to one. The control net is

An alternate form is
![]()
where
![]()
and
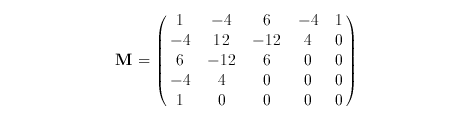
2002.12.07
The surface is defined by the function
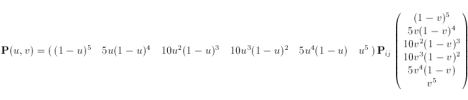
where u and v vary in the range from zero to one. The control net is

An alternate form is
![]()
where
![]()
and

2002.12.07
For some quadratic function f(t)
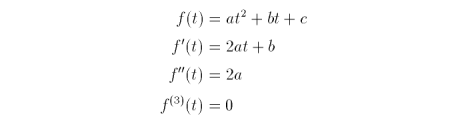
The Taylor series, where k varies in the range from zero to one, is
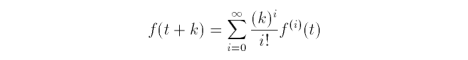
so,
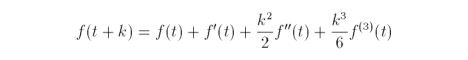
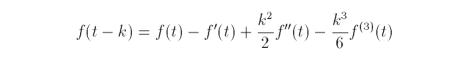
Adding f(t + k) and f(t - k) yields
![]()
Solving for f(t) we get

If g(t) is the second derivative of f(t), then
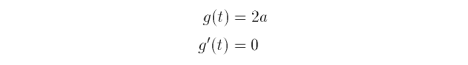
The Taylor series, where k varies in the range from zero to one, is
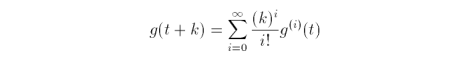
so,
![]()
![]()
Adding g(t + k) and g(t - k) yields
![]()
Solving for g(t) we get
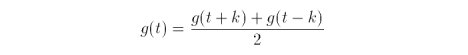
Since we mentioned earlier that g(t) is the second derivative of f(t)
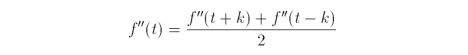
Evaluating successive function values using the central differences is known as central differencing. The psuedocode to evaluate a function of one variable is
compute initial conditions f(0), f(1), f''(0), f''(1) let t = 0.5 let k = 0.5 let E = a very small number less than k function centralDiff(t, k) if (k is less than E) return compute f''(t) compute f(t) display f(t) k = k * 0.5 centralDiff(t - k, k) centralDiff(t + k, k) done
The methodology to determine the central differences of a univariate function can be adapted for a function of two variables. Evaluating a bivariate function usually involves holding one paramater constant while iterating the other parameter from zero to one. Consider the biquadratic function
![]()
or written in matrix form,
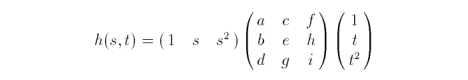
Extending the logic from the one dimensional case, we get the following equations where s is held constant
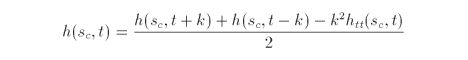
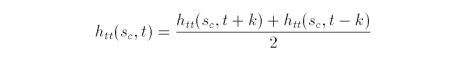
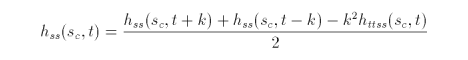
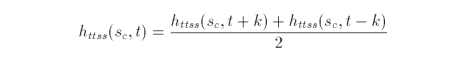
Similarly, when t is held constant

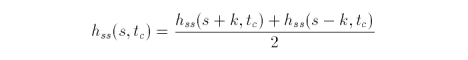
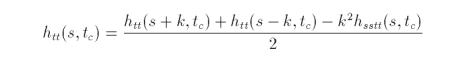
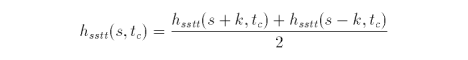
The first and second partial derivatives of the biquadratic function in s and t are
![]()
![]()
![]()
and
![]()
![]()
![]()
With these equations we have enough information to evalaute h(s, t). At the initialisation phase we need to calculate h(0, 0), h(1, 0), h(1, 1) and h(0, 1). We also need the second partial derivatives in both s and t for s = 0,1 and t = 0,1. From these values the biquadratic function h(s, t) can be evaluated efficiently beginning with k = 0.5. With each successive recursive call, k is reduced by half. Recursion stops when k is less than some fixed value.
2003.12.16
//---------------------------------------------------------
// typedefs.h
//---------------------------------------------------------
#pragma once // visual studio .net
#ifndef __TYPEDEFS_H__ // gcc
#define __TYPEDEFS_H__ //
// Red Green Blue (Alpha) model
//
// all components have the range [0, 1]
//
typedef struct {
double r, g, b, a;
} RGB;
// Hue Saturation Value model
//
// H - ranges from 0 to 360 degrees.
// S - degree of strength or purity. range [0, 1]
// V - brightness. range [0, 1], v = 0 is black
//
typedef struct {
double h, s, v;
} HSV;
// Perceived luminance (Y)
// Colour information (I)
// Luminance information (Q)
//
// colour model for NTSC television broadcasts.
//
// Y - fixed bandwidth of 4.2MHz bandwidth for 525 lines
// I - bandwidth range [1, 1.5], usually 1 MHz
// Q - bandwidth range [0.6, 1], usually 1 MHz
//
typedef struct {
double y, i, q;
} YIQ;
// CIE XYZ colour model ( http://www.colour.org/ )
//
typedef struct {
double x, y, z;
} XYZ;
// RGB -> YIQ conversion matrix
//
static double m0[3][3] = {
{0.299, 0.587, 0.114},
{0.596, -0.275, -0.321},
{0.212, -0.523, 0.311}
};
// YIQ -> RGB conversion matrix
//
static double m1[3][3] = {
{1.0, 0.956, 0.621},
{1.0, -0.272, -0.647},
{1.0, -1.105, 1.702}
};
// RGB -> XYZ conversion matrix
//
static double m2[3][3] = {
{0.412453, 0.357580, 0.180423},
{0.212671, 0.715160, 0.072169},
{0.019334, 0.119193, 0.950227}
};
// XYZ -> RGB conversion matrix
//
static double m3[3][3] = {
{ 3.240479, -1.537150, -0.498535},
{ -0.969256, 1.875992, 0.041556},
{ 0.055648, -0.204043, 1.057311}
};
#endif // __TYPEDEFS_H__
//---------------------------------------------------------
// ColourConverter.h
//---------------------------------------------------------
#pragma once // visual studio .net
#ifndef __COLOUR_CONVERTER_H__ // gcc
#define __COLOUR_CONVERTER_H__ //
#include <math.h> // gcc: compile with -lm option
#include "typedefs.h"
class ColourConverter {
public:
ColourConverter() { }
void RGBtoHSV(RGB *, HSV *);
void HSVtoRGB(HSV *, RGB *);
void RGBtoYIQ(RGB *, YIQ *);
void YIQtoRGB(YIQ *, RGB *);
void RGBtoXYZ(RGB *, XYZ *);
void XYZtoRGB(XYZ *, RGB *);
private:
double minVal(double, double, double);
double maxVal(double, double, double);
};
inline double
ColourConverter::minVal(double a, double b, double c)
{
if (a < b && a < c) return a;
if (b < a && b < c) return b;
if (c < a && c < b) return c;
return a;
}
inline double
ColourConverter::maxVal(double a, double b, double c)
{
if (a > b && a > c) return a;
if (b > a && b > c) return b;
if (c > a && c > b) return c;
return a;
}
#endif // __COLOUR_CONVERTER_H__
//---------------------------------------------------------
// ColourConverter.cpp
//---------------------------------------------------------
#include "ColourConverter.h"
void ColourConverter::RGBtoHSV(RGB *source, HSV *target)
{
double r = source->r;
double g = source->g;
double b = source->b;
double min = minVal(r, g, b);
double max = maxVal(r, g, b);
double delta = max - min;
// v
target->v = max;
if (max != 0.0)
// s
target->s = delta / max;
else {
// r = g = b = 0
// s = 0, v is undefined
target->s = 0;
target->h = -1;
return;
}
if (r == max) {
// between yellow & magenta
target->h = (g - b) / delta;
} else if (g == max) {
// between cyan & yellow
target->h = 2 + (b - r) / delta;
} else {
// between magenta & cyan
target->h = 4 + (r - g) / delta;
}
// degrees
target->h *= 60;
if(target->h < 0) target->h += 360;
}
void ColourConverter::HSVtoRGB(HSV *source, RGB *target)
{
int i;
double f, p, q, t;
double h = source->h;
double s = source->s;
double v = source->v;
if (s == 0.0) {
// achromatic (gray)
target->r = v;
target->g = v;
target->b = v;
return;
}
h /= 60; // sector 0 to 5
i = floor(h);
f = h - i; // factorial part of h
p = v * (1.0 - s);
q = v * (1.0 - s * f);
t = v * (1.0 - s * (1.0 - f));
switch (i) {
case 0:
target->r = v;
target->g = t;
target->b = p;
break;
case 1:
target->r = q;
target->g = v;
target->b = p;
break;
case 2
target->r = p;
target->g = v;
target->b = t;
break;
case 3:
target->r = p;
target->g = q;
target->b = v;
break;
case 4:
target->r = t;
target->g = p;
target->b = v;
break;
default: // case 5:
target->r = v;
target->g = p;
target->b = q;
break;
}
}
void ColourConverter::RGBtoYIQ(RGB *src, YIQ *tar)
{
tar->y=m0[0][0]*src->r+m0[0][1]*src->g+m0[0][2]*src->b;
tar->i=m0[1][0]*src->r+m0[1][1]*src->g+m0[1][2]*src->b;
tar->q=m0[2][0]*src->r+m0[2][1]*src->g+m0[2][2]*src->b;
}
void ColourConverter::YIQtoRGB(YIQ *src, RGB *tar)
{
tar->r=m1[0][0]*src->y+m1[0][1]*src->i+m1[0][2]*src->q;
tar->g=m1[1][0]*src->y+m1[1][1]*src->i+m1[1][2]*src->q;
tar->b=m1[2][0]*src->y+m1[2][1]*src->i+m1[2][2]*src->q;
}
void ColourConverter::RGBtoXYZ(RGB *src, XYZ *tar)
{
tar->x=m2[0][0]*src->r+m2[0][1]*src->g+m2[0][2]*src->b;
tar->y=m2[1][0]*src->r+m2[1][1]*src->g+m2[1][2]*src->b;
tar->z=m2[2][0]*src->r+m2[2][1]*src->g+m2[2][2]*src->b;
}
void ColourConverter::XYZtoRGB(XYZ *src, RGB *tar)
{
tar->r=m3[0][0]*src->x+m3[0][1]*src->y+m3[0][2]*src->z;
tar->g=m3[1][0]*src->x+m3[1][1]*src->y+m3[1][2]*src->z;
tar->b=m3[2][0]*src->x+m3[2][1]*src->y+m3[2][2]*src->z;
}
